счетность множества действительных чисел

[AD]

Там вся "отпротивность" заложена в последней строчке. Типа некоторое рассуждение, а потом "если бы мы в самом начале предположили, что множество действительных чисел счетно, то нашелся бы список, содержащий все действительные числа, а мы уже умеем доказать, что никакой список множество действительных чисел не накрывает". Изначально не предполагается, что в списке содержатся все действительные числа. Просто берется любой список каких-нибудь действительных чисел - и оказывается, что он заведомо не полон.

[MaximKat]

Sla_sh писал(а):

Сам же такие мысли и высказывал, но разные индивидуумы, например, PAV говорили, что совсем эти дроби и не бесконечны - вполне могут быть и конечными. И вроде как совсем и не важно конечны они или нет.

Конечная дробь, это если с некоторого места одни нули идут В бесконечном количестве

[Sla_sh]

id писал(а):

Sla_sh
Ну как же, не от противного?
Говорится, что множество несчетно. Допустим, что это не так, т.е., что оно счетно. Раз счетно, значит, можно "выписать", ну и дальше все строится.
Что, противоречие? Значит, оно несчетно.

Ай...дадада, логично. Это я туплю.

Мысль в том, что противоречия никакого нет. Потому что любое число с конечным набором разрядов входит в исходное множество, т.к. ему в соответствие можно поставить номер по алгоритму, приведенному в первом сообщении темы.

Ну, то есть, если брать все конечные числа до второго разряда - получим:
1 - 0,1
2 - 0,2
3 - 0,3
...
9 - 0,9
10 - 0,11
11 - 0,12
18 - 0,19
и т. д.

То есть, как ни строй диагональной процедурой Кантора число с конечным количеством разрядов - оно все равно будет иметь порядковый номер из натурального ряда.

А почему для чисел с бесконечным количеством разрядов ситуация изменится я не понимаю.
Это наверное почти как в той истории: то, что парралельные прямые не пересекаются я понимаю, но не понимаю почему.

[ewert]

Sla_sh писал(а):

но разные индивидуумы, например, PAV говорили, что совсем эти дроби и не бесконечны - вполне могут быть и конечными. И вроде как совсем и не важно конечны они или нет.

Да не мог PAV такого говорить. Он, насколько я помню, постоянно талдычил одно: что у Вас, в Вашем алгоритме дроби исключительно конечны -- в то время как они запросто могут быть бесконечными. Ну так это святая правда.

Sla_sh писал(а):

Да не было там такого. Вы доказательство читали? Он же ж не от противного доказывает...

Он (в данном случае Колмогоров) -- именно от противного. От исключительно противного.

Sla_sh писал(а):

Ну и конечно назревает вопрос: а зачем нам вообще нужны числа, которые написать невозможно?

А вот это -- уже вопрос по существу. И ответ -- двоякий.

1). Да, нужны, ибо нам нужна полнота (называйте её аксиомой или теоремой -- как угодно, лишь бы она была). Ибо без неё теория пределов не складывается. А без неё невозможно корректно описывать физические процессы, к примеру. Ну а это уж жизненно грустно.

2). Что значит -- невозможно? Возможно в математике всё, лишь бы не было противоречиво. Ну так определение вещественных чисел и непротиворечиво, и вполне адекватно обслуживает практику. Чего ещё желать?

Добавлено спустя 3 минуты 50 секунд:

Sla_sh писал(а):

А почему для чисел с бесконечным количеством разрядов ситуация изменится я не понимаю.

Ну попытаюсь: это потому, что изначально Вы рассматриваете только конечные количества разрядов -- и, следовательно, Ваша конструкция в принципе неспособна обслужить бесконечные.

Это убедительно?

[Sla_sh]

MaximKat писал(а):

Sla_sh
Давайте на примерах попробуем. На конечных разумеется Smile

Рассмотрим множество $\{0.12345,0.11111,0.23223,0.56456,0.43545\}$. Теперь мы будем строить число с 5 знаками после запятой, которого нет в этом множестве. Смотрим первую цифру первого числа, она равна 1. Поэтому первой цифрой нашего числа будет 2. Вторая цифра второго числа равна опять 1, значит мы снова берем 2. Третья цифра третьего числа равна 2, поэтому мы берем 1. Аналогично, 4 и 5 цифры будут 2. Т.е. мы каждый раз берем 2, если только в n-ом числе на n-ом месте не 2, иначе берем 1.
Получили число 0.22122, которого нет в исходном множестве.

Абсолютно так же, если брать счетное множество и бесконечные дроби (в которых количество знаков тоже счетное) можно построить дробь, которой в исходом множестве не было.
Вопросы есть?

ну так постройте ж все возможные комбинации от 0,00001 до 0,99999 и включите их в множество.
первое число - 0,00001, второе - 0,00001+0,00001=0,00002, третье - 0,00002+0,00001 = 0,00003 и так до 0,99999

Никакая диагональная процедура Кантора вам не поможет...

AD писал(а):

Там вся "отпротивность" заложена в последней строчке. Типа некоторое рассуждение, а потом "если бы мы в самом начале предположили, что множество действительных чисел счетно, то нашелся бы список, содержащий все действительные числа, а мы уже умеем доказать, что никакой список множество действительных чисел не накрывает". Изначально не предполагается, что в списке содержатся все действительные числа. Просто берется любой список каких-нибудь действительных чисел - и оказывается, что он заведомо не полон.

Дада, согласен. Спасибо, что разъяснили.

[MaximKat]

Sla_sh писал(а):

ну так постройте ж все возможные комбинации от 0,00001 до 0,99999 и включите их в множество.
первое число - 0,00001, второе - 0,00001+0,00001=0,00002, третье - 0,00002+0,00001 = 0,00003 и так до 0,99999
Никакая диагональная процедура Кантора вам не поможет...

Когда мы строим наше число, то его m-ый разряд строится на основе m-ого разряда m-ого числа исходного множества. Т.е. "множество разрядов дроби" (понятно что я имею ввиду?) должно быть равномощно исходному множеству множеству. А у Вас разрядов 5, а чисел в исходном множестве 99999. Так что фигушки.

Если же рассматривать все дроби как бесконечные, т.е. 0.00001=0.00001000...., ..., 0.99999=0.99999000..., то получится число 0.1111111111..., которого в исходном множестве нет.

Sla_sh писал(а):

А почему для чисел с бесконечным количеством разрядов ситуация изменится я не понимаю.

Да вот поэтому и измениться. Чтобы этот алгоритм можно было применять к бесконечному исходному множеству нужно бесконечное число разрядов.

[Sla_sh]

Цитата:

Да не мог PAV такого говорить. Он, насколько я помню, постоянно талдычил одно: что у Вас, в Вашем алгоритме дроби исключительно конечны -- в то время как они запросто могут быть бесконечными. Ну так это святая правда.

Не буду сейчас искать - сложно это по дайл апу. Дискуссия вроде в правильном русле пошла, так что пока это и не важно.

Цитата:

1). Да, нужны, ибо нам нужна полнота (называйте её аксиомой или теоремой -- как угодно, лишь бы она была). Ибо без неё теория пределов не складывается. А без неё невозможно корректно описывать физические процессы, к примеру. Ну а это уж жизненно грустно.

точно! как я сам-то не сообразил? ) спасибо)

Цитата:

Ну попытаюсь: это потому, что изначально Вы рассматриваете только конечные количества разрядов -- и, следовательно, Ваша конструкция в принципе неспособна обслужить бесконечные.

Это убедительно?

Вполне. Согласен.
Но тогда не понятно, как же мне проследить закономерности в случае бесконечного количества разрядов? По-моему, у Колмогорова это не описано. Или я опять что-то упустил?

То есть, о чем я говорю...Если бесконечность настолько непредсказуема, что для неё конечный аппарат не действует, то как и почему можно вообще утверждать, что вот это сконструированное Колмогоровым число в бесконечности таки не будет входить во множество?

[AD]

Sla_sh писал(а):

ну так постройте ж все возможные комбинации от 0,00001 до 0,99999 и включите их в множество.
первое число - 0,00001, второе - 0,00001+0,00001=0,00002, третье - 0,00002+0,00001 = 0,00003 и так до 0,99999

Никакая диагональная процедура Кантора вам не поможет...

Скажите, Sla_sh, какой номер по вашему алгоритму присваивается числу 1/3. Просто тупо выпишите здесь эту циферку.

[MaximKat]

Sla_sh писал(а):

Если бесконечность настолько непредсказуема, что для неё конечный аппарат не действует, то как и почему можно вообще утверждать, что вот это сконструированное Колмогоровым число в бесконечности таки не будет входить во множество?

Вот почему: чтобы утверждать, что две бесконечные дроби равны нужно сравнить все их разряды, что может быть проблематично А чтобы утверждать, что они не равны, всегда достаточно конечного числа - до первого отличия. Нам нужно как раз показать отличие нового числа от всех старых, так что рассматривать "бесконечные" разряды не нужно

[Sla_sh]

Цитата:

Когда мы строим наше число, то его m-ый разряд строится на основе m-ого разряда m-ого числа исходного множества. Т.е. "множество разрядов дроби" (понятно что я имею ввиду?) должно быть равномощно исходному множеству множеству. А у Вас разрядов 5, а чисел в исходном множестве 99999. Так что фигушки.

Если же рассматривать все дроби как бесконечные, т.е. 0.00001=0.00001000...., ..., 0.99999=0.99999000..., то получится число 0.1111111111..., которого в исходном множестве нет.

Брррр, очень хитро получается.
Понимаете в чем проблема...Дело в том, что даже вот этому числу 0,111111111... с количеством разрядов 99999, насколько я понял, соответствует определенное число из натурального ряда. Опять же, если использовать алгоритм из первого сообщения темы.


Мысли у меня совсем куда-то в дебри полезли, откровенно говоря. Думать надо. И много. Признаюсь честно, я уж и забыл насколько математика интересна.

[Someone]

Sla_sh, если у Вас вызывает трудности логика доказательства "от противного", то вот здесь - доказательство, которое не использует эту логику. А вот здесь - более общее утверждение, которое доказывается тоже без "противного".

Что касается того, что

Sla_sh писал(а):

Но ведь каждому числу из данного множества можно поставить во взаимно однозначное соответствие число из натурального ряда. Например, по следующему алгоритму:
1 - 0,1
2 - 0,2
.....
9 - 0,9
10 - 0,11
11 - 0,12
12 - 0,13
...
18 - 0,19
19 - 0,21
20 - 0,22


Ну и так далее. За несколько минут могу написать программу, которая по натуральному числу вычисляет соответствующее действительное число, а по действительному - натуральное. как же так? Почему множество действительных чисел не счетно?

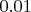
то здесь всё просто, и Вас уже много раз просили сообщить, какой номер в Вашем списке будет иметь, например, число $0.01$, или $\frac 13$, или $\frac{\sqrt{2}}2$. Вы почему-то не отвечаете, а только продолжаете выражать уверенность, что такой номер очень легко найти: "за несколько минут напишу программу". В конце концов, потратьте несколько минут, напишите программу и сообщите нам, наконец, этот номер. И всё встанет на свои места.

P.S. Это не с Вами мы обсуждали этот вопрос на fido7.ru.math года два или три (точно не помню) назад?

Captious писал(а):

А может быть не надо больше продолжения ваших научно-популялялярных лекций?
Всё что вы смогли сказать, уже сказали. Ничего нового мы от вас увы, не услышим.
Повторяю: ваши глюки - это исключительно ваши проблемы.

И не надейтесь. Мои "глюки" - это на 100% Ваши проблемы. С этим согласны и остальные участники обсуждения (Sla_sh и ZVS не в счёт, они разбираются в вопросе не лучше Вас). А в научно-популярных лекциях Вы очень нуждаетесь, так что я продолжу при наличии времени.

Captious писал(а):

г-н Someone Вс Июл 20, 2008 02:58:54 писал(а):

...

В вашем сообщении столько ляпов, непростительных для "профессионала", что подробный их разбор и разъяснения отнимут уйму времени и уведут далеко от обсуждаемого здесь вопроса.
Тем более, что вы по-прежнему совершенно не хотите вникать в аргументы оппонентов и, как всегда, "не можете" найти ничего "существенного" ни у кого, кроме как в написанном самим собой ... :)

Я жду подробного разъяснения "ляпов". Надо же мне усовершенствоваться.

Также с нетерпением жду ответа на вопрос о продвижении по списку "дальше в бесконечность", который я Вам уже дважды задавал.

А пока ещё один замечательный пассаж из Ваших "трудов":

Captious писал(а):

А теперь посмотрим одно из популярных доказательств несчетности множ-ва действительных чисел
Док-во ведется методом от противного.
Известно, что каждое действительное число можно записать в виде бесконечной десятичной дроби вида
А, a1 a2 . . . an . . .

...

Captious писал(а):

Когда первоначально "пересчитывали" элементы, то бесконечные десятичные дроби считали единым и неделимым элементом (= применили абстракцию актуальной бесконечности). А когда решили поискать неохваченное списком "новое" число, то ничтоже сумняшеся, стали каждый элемент рассматривать состоящим из бесконечного количества "элементов второго уровня".
Вот такие вот дела...

А чего же Вы хотите? Вы сами такое представление действительных чисел выбрали - бесконечными десятичными дробями. Раз Вы такое представление выбрали, значит любые его элементы использовать можно. Строим-то мы "элемент первого уровня", а используем ли мы при этом "элементы второго" или ещё какого "уровня" - роли не играет, раз они определены в том "представлении", которое Вы выбрали.

P.S. Цитаты взяты из разных сообщений, но в них обсуждается одно и то же доказательство, просто перекопированное из одного сообщения в другое. Только во втором сообщении исчезла существенная фраза про десятичные дроби, поэтому её пришлось копировать из первого сообщения.

[MaximKat]

Sla_sh писал(а):

Понимаете в чем проблема...Дело в том, что даже вот этому числу 0,111111111... с количеством разрядов 99999, насколько я понял, соответствует определенное число из натурального ряда. Опять же, если использовать алгоритм из первого сообщения темы.

Понятно, что для любого числа можно придумать нумерацию, в которую оно входит Но речь о том, что мы сначала фиксируем исходное множество и номера, а потом уже строим число, которого там нет. Это уже несколько раз здесь упоминали В данном случае рассматривалось множество 0.00001...0.99999

[Sla_sh]

Цитата:

Скажите, Sla_sh, какой номер по вашему алгоритму присваивается числу 1/3. Просто тупо выпишите здесь эту циферку.

ну мы ж это проходили уже.
для бесконечных дробей мой алгоритм не работает.

блин, чет я запутался совсем. если мой алгоритм не работает для бесконечных дробей - это ведь не значит, что их невозможно сосчитать?

по-моему, я что-то упустил.

Цитата:

Вот почему: чтобы утверждать, что две бесконечные дроби равны нужно сравнить все их разряды, что может быть проблематично Smile А чтобы утверждать, что они не равны, всегда достаточно конечного числа - до первого отличия. Нам нужно как раз показать отличие нового числа от всех старых, так что рассматривать "бесконечные" разряды не нужно

Воооо, это уже интересно. Хорошая пища для размышлений. Сейчас буду думать.
Похоже, что это оно. Спасибо

[MaximKat]

Sla_sh писал(а):

блин, чет я запутался совсем. если мой алгоритм не работает для бесконечных дробей - это ведь не значит, что их невозможно сосчитать?

Если честно, то из вашего алгоритма вообще мало, что значит Но их действительно невозможно сосчитать. Возможно поэтому множество называют несчетным

[Someone]

Sla_sh писал(а):

блин, чет я запутался совсем. если мой алгоритм не работает для бесконечных дробей - это ведь не значит, что их невозможно сосчитать?

Вообще говоря, не значит. Но ситуация такая, что, как только Вы укажете новый алгоритм нумерации, как Вам тут же укажут способ построить число, которое этот алгоритм не нумерует. Собственно говоря, способ стандартный, его тут уже восьмую страницу обсуждают. Поэтому алгоритма, который нумерует все действительные числа, не существует.
Кстати, слово "алгоритм" здесь употреблять не совсем хорошо. Это слово имеет вполне определённый смысл, а конструкции, которые здесь рассматриваются, в этом смысле алгоритмами не являются.