Подумалось, что, вообще, наверное, стоит ещё раз обратить внимание тех, кто "не верит в передачу энергии полем", на формулу (она выводится с помощью уравнений Максвелла) для мощности

, проходящей через поверхность (например, плоскость) поперечно пересекающую систему проводов с постоянными токами:
![$P=\int \frac{c}{4 \pi}[\mathbf{E \times B}] \cdot d \mathbf{S}\,= \, \sum \limits_k \varphi_k I_k \, .$ $P=\int \frac{c}{4 \pi}[\mathbf{E \times B}] \cdot d \mathbf{S}\,= \, \sum \limits_k \varphi_k I_k \, .$](https://dxdy-02.korotkov.co.uk/f/1/f/1/1f161956ea8436c943ee5326982e135282.png)
Здесь плотность потока энергии
![$(c/4\pi)[\mathbf{E \times B}]$ $(c/4\pi)[\mathbf{E \times B}]$](https://dxdy-03.korotkov.co.uk/f/e/3/7/e378a80c06652e5b29ab83e62c48068582.png)
полей, имеющихся в пространстве вокруг проводов с постоянным током, проинтегрирована по площади воображаемой бесконечно большой плоскости, пересекающей провода;

— ориентированный элемент площади плоскости.
Поля

и

вдали от проводов пренебрежимо малы, вклад в

даёт поле вокруг проводов. Поле внутри проводов не даёт вклада, так как вектор
![$[\mathbf{E \times B}]$ $[\mathbf{E \times B}]$](https://dxdy-04.korotkov.co.uk/f/3/1/5/3159d87119377b935694ea8b4068a63982.png)
внутри провода направлен к оси провода, а векторы элементов площади

направлены вдоль оси провода. (К тому же, если считать проводники идеальными, то

и

внутри идеальных проводников, так как

где

— плотность тока.)
Индекс

нумерует провода;

— потенциалы на сечениях проводов рассматриваемой плоскостью, они постоянны по поперечному сечению проводов.
(Если к проводам применимо приближение идеальных проводников, то потенциалы проводов

не изменяются от точки к точке и вдоль проводов; так можно считать, когда сопротивления нагрузки намного больше сопротивлений проводов, так что потери электроэнергии в проводах пренебрежимы).
(Вывод формулы)
На форуме вывод этой формулы уже был, см. пост
Muninа
post1053230.html#p1053230 Я только добавлю рисунок для более подробного пояснения вывода:
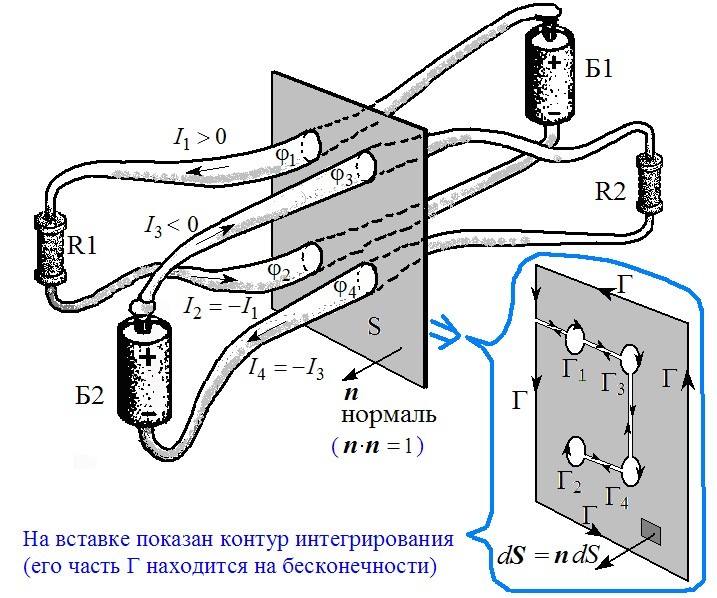
На рисунке: Б1 и Б2 - батарейки; R1 и R2 - резисторы; соединяющие их белые "кишки" изображают голые (без изоляции) провода. Так уж они у меня коряво нарисовалось, извините; требовалось не слишком мелко изобразить сечение проводов, поэтому провода на рисунке такие толстые. Изображён частный случай, но подразумевается общий — с любым количеством пар проводов, по которым постоянные токи текут "туда и обратно".
Рассуждение вот какое. Мысленно проведём поперёк проводов плоскость и выберем направление нормали к ней: например, справа налево. Умножив вектор Пойнтинга
![$(c/4\pi)[\mathbf{E \times B}]$ $(c/4\pi)[\mathbf{E \times B}]$](https://dxdy-03.korotkov.co.uk/f/e/3/7/e378a80c06652e5b29ab83e62c48068582.png)
для удобства на

интегрируем его по всей площади указанной бесконечной плоскости (на рисунке плоскость изображена с краями, но считаем, что эти края расположены бесконечно далеко от проводов; ориентированный элемент площади обозначен вектором

буква

здесь не обозначает вектора Пойнтинга). Тем самым получаем умноженную на

мощность

(это величина с размерностью энергии, делённой на время), проходящую через плоскость; если

то мощность передаётся в направлении нормали, а если

то — в противоположном направлении.
![$(4\pi /c)P=\int [\mathbf{E \times B}]\cdot d\mathbf{S} \, .$ $(4\pi /c)P=\int [\mathbf{E \times B}]\cdot d\mathbf{S} \, .$](https://dxdy-03.korotkov.co.uk/f/e/0/6/e06a9803afdbf85b82bca5cebbd012ee82.png)
Внутри каждого провода вектор Пойнтинга направлен к оси провода (либо его можно считать равным нулю, если проводник считается идеальным), так что сечения проводов нашей плоскостью не дают вклада в этот интеграл. Поэтому вместо интегрирования по всей плоскости можно с тем же результатом интегрировать только по той части плоскости, которая расположена вне проводов. Эта область далее обозначается буквой

на рис. эта область выделена серым цветом. На вставке отдельно показана ориентированная граница

этой области; её участки, обозначены буквами "Г".
Учитывая, что

в случае постоянных (во времени) полей, и что ротор поля

есть
![$[\nabla \times (\varphi \mathbf{B})]= (\nabla \varphi) \times \mathbf{B}+\varphi [\nabla \times \mathbf{B}] \, ,$ $[\nabla \times (\varphi \mathbf{B})]= (\nabla \varphi) \times \mathbf{B}+\varphi [\nabla \times \mathbf{B}] \, ,$](https://dxdy-03.korotkov.co.uk/f/e/1/2/e1279adabe04f4d86f71108cd6c8412c82.png)
получаем:
![$(4\pi /c)P=-\int \limits_S [\nabla \times \varphi \mathbf{B}] \cdot d\mathbf{S}+\int \limits_S \varphi [\nabla \times \mathbf{B}] \cdot d\mathbf{S} \, .$ $(4\pi /c)P=-\int \limits_S [\nabla \times \varphi \mathbf{B}] \cdot d\mathbf{S}+\int \limits_S \varphi [\nabla \times \mathbf{B}] \cdot d\mathbf{S} \, .$](https://dxdy-01.korotkov.co.uk/f/8/5/8/85856de105f55a8ca15f3511d58ad9a982.png)
Во втором слагаемом подынтегральное выражение равно нулю, так как согласно уравнению Максвелла
![$[\nabla \times \mathbf{B}]=\frac{1}{c} \frac{\partial \mathbf{E}}{\partial t} +\frac{4\pi}{c}\mathbf{j} \, ,$ $[\nabla \times \mathbf{B}]=\frac{1}{c} \frac{\partial \mathbf{E}}{\partial t} +\frac{4\pi}{c}\mathbf{j} \, ,$](https://dxdy-03.korotkov.co.uk/f/e/8/4/e848dc1fbe2032db0077d48be9e78eca82.png)
но у нас

в области

(область вне проводов) и

(поля постоянные).
Первое слагаемое преобразуем по теореме Стокса в интеграл по границе области
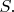
Таким образом:

Границу можно предствить (см. рис.) как сумму отрезков, которые проходятся дважды, но в противоположных направлениях и поэтому не дают вклада в интеграл, плюс окружности

плюс внешний контур

который находится на бесконечности и не даёт вклада в интеграл, так как поля быстро убывают с расстоянием вдали от проводов. Другими словами, остаётся только вклад от окружностей

т.е. от ориентированных линий пересечения поверхности проводов с рассматриваемой поперечной к проводам плоскостью.
Можно считать, что потенциал в проводе не изменяется от точки к точке в поперечном сечении провода, поэтому его можно вынести за знак интеграла. Заодно изменим знак всего выражения, изменив направление обхода окружностей

. Получаем:

Окружности с изменённой ориентацией,

являются границами кружков

— поперечных сечений проводов; у них нормали ориентированы так же, как нормаль исходной плоскости. Пользуясь теоремой Стокса и уравнением Максвелла, можем записать:
![$\oint \limits_{-\Gamma_k} \mathbf{B} \cdot d\mathbf{l}= \int \limits_{S_k}[\nabla \times \mathbf{B}]\cdot d\mathbf{S}=\frac{4\pi}{c} \int \limits_{S_k} \mathbf{j}_k\cdot d\mathbf{S}=\frac{4\pi}{c}I_k \, .$ $\oint \limits_{-\Gamma_k} \mathbf{B} \cdot d\mathbf{l}= \int \limits_{S_k}[\nabla \times \mathbf{B}]\cdot d\mathbf{S}=\frac{4\pi}{c} \int \limits_{S_k} \mathbf{j}_k\cdot d\mathbf{S}=\frac{4\pi}{c}I_k \, .$](https://dxdy-01.korotkov.co.uk/f/c/5/0/c50090d10f8d24d95eba405b4c38cd4c82.png)
Таким образом:
![$P=\frac{c}{4\pi}\int \limits_S [\mathbf{E \times B}] \cdot d\mathbf{S}=\sum \limits_k \varphi_k I_k \, .$ $P=\frac{c}{4\pi}\int \limits_S [\mathbf{E \times B}] \cdot d\mathbf{S}=\sum \limits_k \varphi_k I_k \, .$](https://dxdy-04.korotkov.co.uk/f/b/0/b/b0b5e39603a56f14890152650e176bf582.png)
Эта формула, с одной стороны, выявляет связь мощности

"передаваемой по проводам" через поперечную к проводам плоскость, с картиной полей

и

на этой плоскости вокруг проводов. Тем самым обосновывается картина "полевой передачи электроэнергии" — полями вокруг проводов. С другой стороны, мы видим, что та же самая мощность

с тем же правом (в случае постоянных токов) может быть выражена через потенциалы и токи проводников — этот факт служит основанием для удобной в инженерной практике "электротехнической" точки зрения: "электроэнергия передаётся током по проводам".
Этой формулой поясняется также инвариантность (казалось бы, парадоксальная) величины

к некоторым изменениям полей

и

Можно изгибать, раздвигать или сдвигать провода, скручивать их синей изолентой, поворачивать или сближать батарейки и резисторы, можно добавлять поля, приближая к проводам посторонние заряженные тела или магниты, — всё это, как показывает опыт, практически не изменяет мощность, потребляемую резисторами от батареек, хотя, как мы себе представляем, может сильно менять пространственную картину полей


Формула объясняет дело так: если батарейки обеспечивают стабильность токов

и потенциалов

(точнее говоря, стабильность разностей потенциалов), то поля, как бы сильно они ни менялись, могут меняться только таким образом, что

заведомо останется неизменной.
Заодно добавлю комментарий к упоминавшемуся примеру с четырьмя проводами, двумя батарейками и резисторами, которым
Александрович как бы пытается "опровергать теоретиков". Этот пример, конечно, не опровергает полевую картину переноса энергии. Просто надо учитывать, что мощность, проходящая через плоскость, поперечную к проводам, и токи в проводах здесь оказываются величинами со знаком: ток

если он течет "по нормали" к ориентированной плоскости, и

если он течёт "против нормали". Аналогично определяется знак мощности

В упомянутом примере

и

поэтому

Обе разности потенциалов здесь положительные (если считать, что "плюсовая" клемма батарейки имеет более высокий потенциал, чем "минусовая"), а токи имеют разный знак, чему и соответствует разный знак обоих вкладов в

Значит, в случае с

нельзя безоговорочно заключать, будто "в резисторы не поступает мощность": прежде надо посмотреть, отличны ли от нуля отдельные вклады

и

в суммарную мощность

Конечно, посмотреть отдельный вклад в мощность проще всего путём измерения тока и разности потенциалов (напряжения) в паре проводов, подключенных к резистору; или даже просто пощупав, греется ли этот резистор :)). Техники так и поступают. А теоретически вычислить поля

и

вокруг конкретного резистора в реальной сложной обстановке и посчитать по ним подводимую к резистору мощность — очень трудно. Но отсюда не следует, будто "теория не сшивается с практикой". Наборот, отлично сшивается, потому что в теории выводится
общий результат: при любой частной конфигурации проводов, батареек и резисторов, поток энергии поля через любую замкнутую поверхность, охватывающую резистор, заведомо будет равен той самой подводимой к резистору мощности, которая определяется "электротехнически", как произведение тока и напряжения.
(Вот этот вывод)
Выкладки здесь почти такие же как в приведённом выше выводе, только воображаемая поверхность, по которой мы интегрируем вектор Пойнтинга, здесь другая. Представим себе вместо плоскости замкнутую поверхность произвольной формы, окружающую интересующий нас резистор; см. рис.:
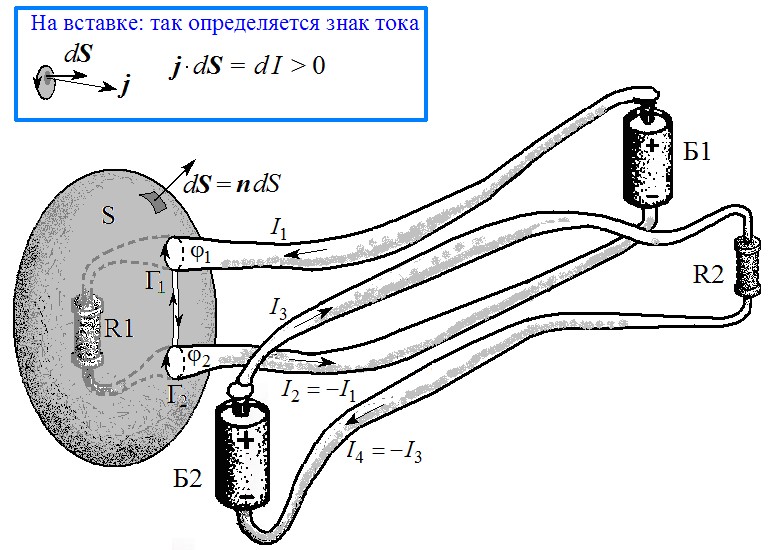
Интегрирование вектора Пойнтинга по ней сводится к интегрированию по площади области
показанной серым цветом (эта область — исходная поверхность с вырезанными кружками-сечениями проводов). Ориентация границы

выбирается так, чтобы "глядя с острия нормали" граница обходилась против часовой стрелки. На рис. нормали ко всем элементам площади выбраны "наружу". При таком выборе нормалей результат

будет означать, что электроэнергия выходит из под поверхности наружу, т.е. внутри поверхности находится батарейка. Если внутри резистор, потребляющий энергию, то

где, как и раньше:
![$P=\frac{c}{4\pi}\int \limits_S [\mathbf{E \times B}] \cdot d\mathbf{S}\, .$ $P=\frac{c}{4\pi}\int \limits_S [\mathbf{E \times B}] \cdot d\mathbf{S}\, .$](https://dxdy-04.korotkov.co.uk/f/7/5/c/75c572ac104edfde8a9d7a32b523c04b82.png)
Как и в предыдущем выводе, интегрирование по площади

сводится к интегрированию по границе. Здесь, в отличие от ситуации в предыдущем выводе, нет бесконечно удалённых участков поверхности. Вклад дают только окружности

, представляющие собой линии пересечения исходной поверхности с поверхностью проводов (см. рис.) Этот вклад по-прежнему сводится к вкладу токов (умноженных на потенциалы), протекающих через кружк
и — сечения проводов. При этом надо учесть, что при выборе нормалей кружков "наружу", границами кружков являются окружности

с противоположным первоначальному направлением обхода; в итоге снова приходим к формуле
![$P=\frac{c}{4\pi}\int \limits_S [\mathbf{E \times B}] \cdot d\mathbf{S}=\sum \limits_k \varphi_k I_k \, .$ $P=\frac{c}{4\pi}\int \limits_S [\mathbf{E \times B}] \cdot d\mathbf{S}=\sum \limits_k \varphi_k I_k \, .$](https://dxdy-04.korotkov.co.uk/f/b/0/b/b0b5e39603a56f14890152650e176bf582.png)
В показанном на рисунке примере имеем:


Поскольку

то получается, как и ожидалось,

по отношению к направлению "наружу".



