Ещё один вопрос. Подскажите пожалуйста, в чём разница между "domain" и "region"? Я и первое, и второе слово перевожу как "область", но возможно это не совсем правильно. Если не трудно, оцените пожалуйста мой перевод маленького текста, насколько он корректно написан?
Оригинал:
"In one spatial dimension, suppose we divide the real line into three distinct pieces using the points x = -1 and x = 1. That is, we define
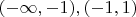
, and
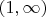
as three separate subdomains of interest, although we regard the first and third as two disjoint pieces of the same region. We refer to
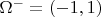
as the inside portion of the domain and
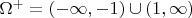
as theoutside portion of the domain."
Мой перевод (я не переводил дословно, просто старался передать смысл):
"Рассмотрим одномерный случай. Разобьём вещественную ось на три неравных промежутка:
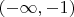
,
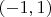
,
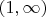
, причём промежутки
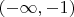
и
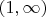
являются разделёнными частями одной и той же области. Назовём
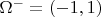
внутренней подобластью, а
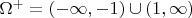
внешней подобластью."



