mod 13#: [3473, 14153, 15811, 26491]
mod 17#: [176641, 224363, 286081, 333803]
mod 19#: [796591, 4260721, 5438903, 8903033]
mod 23#: [8903033, 44237663, 178855141, 214189771]
mod 29#: [401948011, 660375511, 1740505231, 2445118471, 2686017473, 2721352103, 3748341061, 3783675691, 4024574693, 4729187933, 5809317653, 6067745153]
mod 31#: [13341334471, 22095097163, 34088971381, 34793584621, 36096807211, 55541221531, 61975580131, 68721506993, 69426120233, 70506249953, 84507960001, 96385022873, 104175467191, 116052530063, 130054240111, 131134369831, 131838983071, 138584909933, 145019268533, 164463682853, 165766905443, 166471518683, 178465392901, 187219155593]



 есть по крайней мере
есть по крайней мере  .
. 24686821
24686821 19) распадаются на два класса эквивалентности по модулю 13#.
19) распадаются на два класса эквивалентности по модулю 13#. распадаются расположения расстояний d в ПСВ
распадаются расположения расстояний d в ПСВ  ?
? 2
2 .
. в этих ПСВ.
в этих ПСВ. . У меня как раз такая сходимость.Под последовательностью случайных величин рассматривается последовательность расстояний.
. У меня как раз такая сходимость.Под последовательностью случайных величин рассматривается последовательность расстояний. .
. кратный
кратный  . Поэтому максимальное расстояние
. Поэтому максимальное расстояние  получается объединением двух интервалов из ПСВ
получается объединением двух интервалов из ПСВ -
-  и
и  . В этом нет ничего особенного, так как максимальное расстояние в ПСВ
. В этом нет ничего особенного, так как максимальное расстояние в ПСВ и объединяемые интервалы далеки от максимального расстояния.
и объединяемые интервалы далеки от максимального расстояния. максимальное расстояние между вычетами
максимальное расстояние между вычетами  , образуется на стыках меньших ПСВ.
, образуется на стыках меньших ПСВ. увеличиваются расстояния между вычетами ПСВ
увеличиваются расстояния между вычетами ПСВ , как в примере выше.
, как в примере выше. является медленно растущей функцией
является медленно растущей функцией  , где
, где 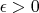 .
.