"Опыт второй был поставлен чешскими физиками. На полированную поверхность массивного кристалла железа наносилась капля расплавленного свинца. Железо было раскалено до температуры более

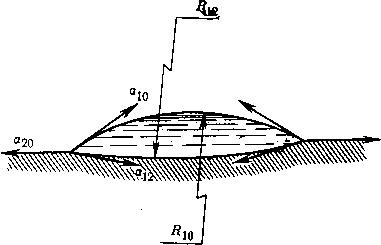
С, и поэтому свинцовая капля оставалась жидкой. Кристалл железа — не полимерная пленка, и изогнуть его вокруг себя капля не может. Поэтому поступает она иным способом: выкапывает под собой ямку такой формы, чтобы вдоль контуров капли все три силы скомпенсировались так, как показано на рисунке. Эта «удобная» ямка должна иметь такую форму, чтобы давление, обусловленное изогнутой поверхностью жидкий свинец — воздух, было в точности равно тому давлению, которое обусловлено искривленностью поверхности жидкий свинец — твердое железо, т. е. дна ямки.
Равенство двух этих давлений означает, что

. Итак, давления равны, а кривизна двух поверхностей различна, потому что различны соответствующие поверхностные энергии.
Выкопав под собой ямку, капля как бы перенеслась в невесомость — как и в невесомости, капиллярное давление оказалось одинаковым вдоль всей поверхности, ограничивающей каплю.
Естественно возникает вопрос: каким образом капля выкопала ямку? Ответим на него. Вначале, когда капля была расположена на плоской поверхности железа, она прижималась к нему тем давлением, которое обусловлено искривленностью поверхности свинец — воздух. Под влиянием этого давления железо из-под свинцовой капли перемещалось в области вокруг нее. Перемещалось в процессе диффузии поатомно, атом за атомом — опыт ставился при высокой температуре, когда диффузия в железе происходит достаточно активно
"
Я.Е. Гегузин АН СССР "Капля"
-- 22.06.2015, 16:53 --там же
"В описанном опыте, вопреки известной пословице, нам удалось убить двух зайцев: определить, во-первых, температуру плавления и, во-вторых, величину поверхностного натяжения расплавленного вещества. Дело в том, что верхняя пластинка, раздавливая своей тяжестью каплю, превращала ее в лепешку определенной толщины. Сколько раз ни повторялся бы опыт по расплавлению одной и той же крупинки, образовывавшаяся жидкая капля весом пластинки расплющивалась до одной и той же толщины к . Эту величину можно было уменьшить, увеличивая вес верхней пластинки. Легко понять, что дальнейшему
расплющиванию препятствуют силы поверхностного натяжения, приложенные к той части поверхности расплющенной капли, которая граничит с воздухом. В наших опытах вещество капли практически не смачивало кварц (именно поэтому опыты и ставились с кварцевыми пластинками) и, следовательно, можно считать, что радиус закругления свободной поверхности

Величина поверхностного натяжения

может быть определена из условия равенства давления, которое оказывает пластинка на жидкую каплю (

), и лапласовского давления (

), которое обусловлено искривленностью ее свободной поверхности. Если вес пластинки давит на каплю с силой

, а площадь ее контакта с расплющенной каплей

, то

. Величина

Приравнивая

к

, находим формулу, с помощью которой можно определить величину поверхностного натяжения вещества:

Величины

и

можно измерить с большой точностью, а силу легко определить, зная вес верхней пластинки
"



