Почему шутки воспринимаются как издевательство

[provincialka]

Yadryara в сообщении #1697041 писал(а):

Попробуйте посмеяться над собой. Очень уважаю это умение.

Я воспринимаю это как "хорошо, если Я могу посмеяться над собой". Но никак не "он(а)". Это личное дело каждого.

Yadryara в сообщении #1697029 писал(а):

Но не только не убедил, так ещё и из Цитатника этот пост удалили и весь разговор вроде тоже.

Если я вижу, что моя шутка неприятна адресату, я извинюсь и буду чувствовать себя неловко. А отнюдь не советовать ему, как ему воспринимать шутки.

[Combat Zone]

Про эмпатию ожидаемо не зашло.

Yadryara
Я пару слов скажу про стартовый пост. И вот этот. post1697029.html#p1697029 Почему шутки не воспринимаются.
Чаще всего все еще проще, чем сказал Sender. Просто люди приходят за разным и существуют на разной волне. И когда одни отдыхают (ничего не имею против, они пришли отдохнуть), другие заняты вполне серьезными вещами. С одной волны на другую переключаться тяжко и не надо, каждому свое. Но вполне естественно, что это несовпадение влечет непонимание и отторжение. А шутки в профильных разделах принимаются и понимаются только от тех, кто там на постоянных правах и по делу.

Ну представьте, что вы напряженно над чем-то думаете, а тут над вами кто-то шутит. В лучшем случае, вы не услышите.

Ваш вопрос многослойный. Какие шутки не воспринимаются? Когда шутить неуместно? С кем лучше не шутить? С кем шутить допустимо? Ну и так далее, у вас фантазия богатая, продолжите.

Я могу для себя только на часть ответить (повторюсь, это для себя и только в определенном контексте). Лучше никогда не шутить онлайн с человеком, вам незнакомым. Вы не видите реакцию.

[Yadryara]

provincialka в сообщении #1697050 писал(а):

я извинюсь и буду чувствовать себя неловко. А отнюдь не советовать ему, как ему воспринимать шутки.

А я сделаю и то и другое.

Приношу свои извинения всем кого я невзначай обидел своими шутками.

Прошу постараться воспринимать шутки менее болезненно.

[Dan B-Yallay]

Yadryara в сообщении #1697052 писал(а):

А я сделаю и то и другое.

Приношу свои извинения всем кого я невзначай обидел своими шутками.

Прошу постараться воспринимать шутки менее болезненно.

А потом внимательно слушаете, куда Вам надлежит проследовать вместе со своими шутками, извинениями и пояснениям к ним.

У меня сложилось впечатление, что у нас с Вами юмор одного сорта и Вы поймёте, что это тоже шутка.

[provincialka]

Yadryara в сообщении #1697052 писал(а):

Прошу постараться воспринимать шутки менее болезненно.

Не надо. Лучше вообще не шутите над людьми: видите же, что у вас не получается!

[waxtep]

Yadryara в сообщении #1697047 писал(а):

И что? Тема вроде не об этом.

Тема явно имеет оттенок о морали, соглашусь. Но какова природа явления, вызвавшая эту дискуссию? Я (косвенно) высказал свою гипотезу: речь не о первом детском кораблике, а о десятилетиями возводимом Титанике; и Титаник сей в наших водах уже плавал, разбиваясь о скалы и айсберги математической строгости...

А по самой теме, мне Ваша шутка не кажется издевательством. Возможно, потому что привык к шуткам более грубым и ранящим, а может в силу своей варварской дикости. Сам, честно говоря, хотел тоже что-нибудь подобное ляпнуть, просто не нашёл в моменте чего-то достаточно на свой вкус остроумного, а потом дела отвлекли

[Yadryara]

Combat Zone в сообщении #1697051 писал(а):

Ну представьте, что вы напряженно над чем-то думаете, а тут над вами кто-то шутит. В лучшем случае, вы не услышите.

Ну да, сразу может и не услышу, но потом оценю.

Dan B-Yallay, окей

provincialka в сообщении #1697055 писал(а):

Лучше вообще не шутите над людьми: видите же, что у вас не получается!

В смысле не получается? Вы хотели сказать не всегда получается?

Combat Zone в сообщении #1697051 писал(а):

Лучше никогда не шутить онлайн с человеком, вам незнакомым.

Именно потому, что жизнь сложная штука, лучше избегать слово "никогда".

Не, мне Ваш совет не нравится. Понятно, что есть интересные занятия, и отсутствие шуток необязательно означает скукоту.

Тут ещё непонятно что такое незнакомый человек. Вот бывало живёшь с человеком много лет, думаешь что знаешь его, а он берёт и предаёт тебя. Получается тогда, что все люди незнакомые...

Это же здорово, если человек прекрасно понимает шутки, в том числе над собой (это важно, над другими-то смеяться многие горазды) и шутит в ответ. Ну а как проверить? Аккуратно расспрашивать, нравится ли Вам, когда над Вами шутят, присуща ли Вам самоирония?

Ну можно конечно и так. Вспомните Незнайку

[Combat Zone]

Чтобы избежать аккуратных расспросов, вот так прям сразу и отвечу. Самоирония мне присуща. Чужую могу не понять. Не обязательно над собой, вообще.

Yadryara в сообщении #1697057 писал(а):

Тут ещё непонятно что такое незнакомый человек.

Да, непонятно. Вы хотите об этом поговорить тоже?

Yadryara в сообщении #1697057 писал(а):

Понятно, что есть интересные занятия, и отсутствие шуток необязательно означает скукоту.

Вот именно.

[Yadryara]

Combat Zone в сообщении #1697058 писал(а):

Да, непонятно. Вы хотите об этом поговорить тоже?

Не особо

waxtep в сообщении #1697056 писал(а):

Тема явно имеет оттенок о морали, соглашусь.

О морали можно спорить бесконечно. Посему не об этом спрашиваю, а об особенностях восприятия. Может это к спецам-психологам (которых вроде почти нет на форуме) вопрос. Почему человек чувствует боль, когда шутят в его адрес?

Combat Zone в сообщении #1697058 писал(а):

Самоирония мне присуща.

Не замечал, но всё, видимо, впереди

[Combat Zone]

Так вы со мной и не знакомы.

Yadryara в сообщении #1697059 писал(а):

Не замечал, но всё, видимо, впереди

Надеюсь, не все.

[EminentVictorians]

Yadryara писал(а):

А я вот решил проблему Деления на два Нулём способов, уверен что это многих интересует.

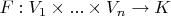
В этой шутке забавно то, что деление на 2 действительно иногда связано с делением на 0 (в тех ситуациях, когда $2 = 0$, в полях характеристики 2 например). Более того, это может быть неплохой такой проблемой, вполне математической. Есть у нас полилинейная форма $F: V_1 \times ... \times V_n \to K$ ($V_i$ - векторные пространства над полем $K$). Для нее определить кососсимметричность хочется так: форма кососимметрична, если при перестановке любых двух аргументов она меняет знак. Подумем, что будет, если скормить такой форме тупель $(v_1, ..., v_i, ... ,v_j, ..., v_n)$, в котором $v_i = v_j$. 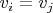Получаем:

$$F(v_1, ..., v_i, ... ,v_j, ..., v_n) = a = F(v_1, ..., v_j, ... ,v_i, ..., v_n) = -a $$

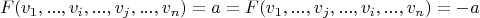
Получается, что $a = -a$, значит $a = 0$. Получили хорошее свойство: кососимметричная полилинейная форма обнуляется на кортеже, содержащем пару равных векторов.

Кто читал внимательно, сразу же заметил ошибку в этом рассуждении. А именно: получили мы, что $a = -a$. Но следует ли отсюда, что $a = 0$?

$$a = -a$$

$$a + a = 0$$

$$2a = 0$$

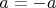
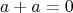
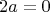
И все. Дальше нельзя сделать вывод о том, что $a = 0$, потому что в поле характеристики 2 это не обязательно. Получается, что в полях характеристики 2 из таким образом (как выше) определенной кососимметричности не следует, что кососимметричная форма будет обнуляться на кортежах, содержащих одинаковые вектора.

Именно из-за этой подставы с характеристикой = 2 кососимметричность определяют по другому: полилинейная форма называется кососимметричной, если она обнуляется на любом векторе своих аргументов, среди которых есть равные. Т.е. по сути, просто более сильная версия предыдущего определения.

Так что проблема деления на ноль действительно существует

[Yadryara]

Combat Zone в сообщении #1697060 писал(а):

Так вы со мной и не знакомы.

Ну я имел в виду, что в ваших постах не замечал самоиронии.

А наоборот заметил словечко "вскидываетесь" в отношении меня, хотя я совершенно не вскидывался. Может как раз шутка была, которую я не понял

Вот у EminentVictorians отличная шутка: якобы не заметил, что тема в Свободном Полёте, а не в Математике

[EminentVictorians]

Yadryara в сообщении #1697063 писал(а):

Вот у EminentVictorians отличная шутка: якобы не заметил, что тема в Свободном Полёте, а не в Математике

Я просто просох после развода с теорией множеств, давно на форум не писал, дискуссионный зуд. Поэтому мне уже пофигу в какую тему писать

[Утундрий]

Цитата:

Почему шутки воспринимаются как издевательство?

Потому что шутки и есть издевательство.

[Yadryara]

Но тогда и издевательство надо воспринимать как шутку и не обижаться