А может Вы всё-таки изложите свой вариант?
Ну что вы, я предпочту подождать, пока вы сами откроете учебник. Правда, как показывает опыт, это будет примерно

Это самое правильное решение! А у меня на

терпежа не хватает, и вместо того чтобы, не портя нервы и глаза, покинуть эту скорбную тему, надумал опять встрять (раз уж и в самом начале имел такой грех...)
eprosИтак, опять флуд вместо конкретных замечаний
Не флуд. Вопросы
Muninа впрямь "диагностические": из ответов видно, как у народа обстоит дело с курсом квантовой механики... Пока тема не в пургатории, позвольте сформулирую "конкретные замечания".
Во-первых, в квантовой механике оператор энергии системы это
оператор Гамильтона данной системы. Чтобы в квантовой теории описать рассматриваемую систему, люди в первую очередь аккуратненько записывают её гамильтониан. У разных систем гамильтонианы разные. В случае замкнутой системы или системы в постоянном внешнем поле её гамильтониан не зависит от времени

.
Во вторых, волновую функцию системы не выдумывают с потолка, не "обрезают" и "не дополняют" никакими нулями - эти произвольные манипуляции не имеют отношения к квантовой механике. (И в эксперименте волновая функция системы не измеряется, и к единственному экземпляру системы не относится; она нужна в теории - для расчета вероятностей и средних значений физ. величин.)
Волновая функция должна быть найдена как решение волнового уравнения Шрёдингера. И уж если гамильтониан системы выбран эрмитовым и не зависящим от

, то этим гарантируется, что частные решения можно найти как собственные функции гамильтониана; они (по определению энергии) принадлежат собственным значениям энергии - т.е. строго определённым значениям

в любой момент

. Из частных решений можно составить линейную комбинацию, подобрав её постоянные коэффициенты под заданное начальное условие.
Таким образом, и в частных решениях и в общем решении волнового уравнения Шрёдингера зависимость волновой функции от

полностью детерминирована, поэтому как-то ещё специально убеждаться "в том, что при всех

волновая функция имеет вид «нечто независимое от

», умноженное на мнимую экспоненту от

" вовсе не нужно! Достаточно решить волновое (т.е. временнОе) у.Ш., и внимательно посмотреть на вид получившейся функции: куда и как там входит переменная

.
Теперь, рискуя получить упрёк за разжёвывание, объясняю суть задачки с

(Кстати, нормировочный множитель правильнее было бы выбрать так:
![$\sqrt[4]{2/\pi}$ $\sqrt[4]{2/\pi}$](https://dxdy-01.korotkov.co.uk/f/c/5/4/c54dc53492e702440e790f7a25ab535f82.png)
; но в данной задачке он роли не играет, и его можно вообще не писать или обозначить какой-либо одной буквой, как константу. А показатель экспоненты нагляднее (привычнее для студентов) было бы записать как

, но это тоже не принципиально). Всякий прилежный студент, а может быть даже и троечник, узнает здесь волновую функцию гармонического осциллятора в стационарном состоянии на нижнем уровне энергии - вот быстрый ответ на вопрос, чему равна энергия.
Можно обосновать этот ответ подробнее. Допустим, мы не помним, в каких задачках какие получались ответы. Однако предположим, что заданная
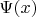
есть собственная функция для какого-то гамильтониана, не зависящего от

(ведь
Munin "суров, но не злонамерен"

.) Замечаем, что она зависит от одной координаты, и эта координата безразмерна (размерная

не могла бы оказаться аргументом не степенной функции), т.е. некий масштаб длины уже принят за единицу. Значит, задача 1-мерная, причём постоянную Планка и массу частицы в у.Ш. тоже можем положить равными единице, так что стационарное у.Ш. должно иметь вид:

Потенциал

мы пока не знаем. Но спокойно берём вторую производную от

и смотрим, что вышло. Видим, что имеет место равенство:

Значит, потенциал

пропорционален

и, стало быть, рассматривается осциллятор. Правда, коэффициент при

отличается от стандартного "1/2" в учебниках, но это лечится заменой переменной

: заменяем исходную

на новую

и в итоге имеем:

Очевидно, что такое же равенство прямо следует при

из у.Ш. для осциллятора (которое каждый студент, изучивший КМ, знает как свои пять пальцев):

где, как известно,

. Значит, заданная нам функция

принадлежит уровню энергии

.
Хорошо. А можно ли признать этот ответ исчерпывающим? Увы, нет... Ведь мы
предположили, что заданная в.ф. -
собственная для частицы в некотором потенциале

. На самом же деле гамильтониан должен быть задан заранее. И если потенциал в нём не имеет вида

, то заданная функция

не будет собственной и должна будет рассматриваться как начальное условие при

для волнового у.Ш.
Для заданного гамильтниана мы нашли бы собственные функции

, спектр

, нашли бы коэффициенты

разложения заданной

по

и построили бы нестационарное решение

как сумму частных решений

. Но, если гамильтониан не задан, то да, педантичный ответ - "недостаточно данных".



