В целом состояние системы, конечно, изменится. Только какое отношение это изменение состояния системы имеет к состоянию колбы?
Прямое: состояние колбы тоже изменится.
Это каким же образом? Напомню, что наблюдатель, делающий измерение состояния колбы не зафиксирует никаких изменений. Нет наблюдаемой разницы в состояниях - нет самой разницы состояний.
Ваш пример - чуть более сложный пример ЭПР-пары. Установка и колба взаимодействуют согласно законам квантовой механики, эволюция волновой функции системы - унитарная. Как бы то ни было, после того как непосредственно они перестали взаимодействовать, но перед тем как Вы начали проводить любые измерения - состояние системы не сепарабельно.
Эх, зря Вы не послушались моего совета – только время зря потратили (и своё и моё) на ответ.

Сепарабельно состояние системы или нет – Алиса всегда может измерить свою часть подсистемы (колбу) и обнаружить, что результаты её измерения абсолютно
не зависят от измерений (или не измерений), проводимых Бобом над устройством. Если нет никакой разницы, то и нет никакого изменения состояния колбы, зависящего от манипуляций Боба. Что здесь непонятно?
Цитата:
Для простоты. Пусть колба может находиться в двух состояниях

и установка в

, Причем унитарная эволюция устроена так, что по окончании ее , т.е. "приготовления" - состояние системы является смесью

(в реальности, конечно, число "степеней свободы" подсистем поболее). Ни о каком "единственном члене" тут речи нет.
Вы взяли слишком простой пример. В нём состояние колбы описывается в виде равной смеси состояний
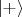
и
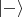
. Я же говорю о более сложном примере, когда состояние колбы описывается в виде суперпозиции, типа волнового пакета, а не смеси. Собственно, любое классическое тело и представляет собой сумму таких волновых пакетов, и описывается именно в
суперпозиции энергетических состояний, так как время приготовления состояния даёт погрешность энергии значительно больше, чем разница уровней энергии классического тела, на что делают ударение в ЛЛ5 стр.29. Сам факт существования определённых размеров у классического тела свидетельствует о суперпозиции состояний.
Собственно говоря, может здесь и нет никакого парадокса внутри КМ, так как есть определённая "лазейка" в виде значительной длительности измерений энергетических состояний классического тела (этот вопрос надо отдельно тщательно изучать). Возможно, при длительных измерениях, любой приготовленный волновой пакет (их сумма) "расползётся" до степени, когда измерение одной из случайных мод первоначальной суперпозиции и этого "расползшегося" волнового пакета, дадут одинаковый результат.
Вот поэтому я написал следующее:
Берём замкнутый ящик с котом. С точки зрения КМ этот ящик описывается всего одной ортогональной волновой функцией (энным уровнем энергии этого ящика с котом). Эта волновая функция описывает не кота, а кучку пепла с вонючим газом, и, с точки зрения КМ, кот в ящике уже мёртвый, как только мы закрыли крышку ящика. И здесь нет никакого парадокса, потому что измерение этого, энного уровня энергии, требует столько времени, что, по прошествии этого времени кот уже будет иметь именно такой вид.
Ув.
Muninу не понравилось такое «крутое» определение кота Шредингера, и он потребовал доказательств, которые и были предоставлены

.
(Оффтоп)
Цитата:
Я, скорее за, чем против (попробуйте предложить в разделе "работа форума").
Не думаю, что этот пункт будет принят и выполняться, так как это требует значительных усилий по изменению стиля общения, прежде всего, самих модераторов. Вот если сами постоянные участники захотят что-то изменить, тогда и будет определённый прогресс.