Вот изначальная система.

Очевидно, что новые переменные это

и

.
Новая система это:

А далее выражение одной переменной через другую в виде

.
Что приводит к тому самому

. Ну и я, видимо, здесь ошибаюсь, так как у меня вызывает этот момент затруднение в понимании. При

, если
 не
не чётное число, то

, так? Если основание степени

с минусом, а показатель степени число не чётное, то произведение тоже с минусом. Вроде должно приводить к

, но правильное решение будет только если
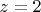
. Таков ход моего решения полностью.
-- 22.05.2025, 18:37 --Иными словами, всё сводится к разрешению уравнения

. Как его правильно решать?
-- 22.05.2025, 18:43 --(Кстати, почему-то не работает знак "умножение" после числа с показателем степени. Например:

. Это так z^3\cdott отображается).



