Пересечение сведётся к одному множеству всех частей. Т.е. не будет представлять вполнепорядок.
Начхать. В доказательстве никаким способом не используется количество цепей, то есть, совершенно не важно, одна такая цепь или не одна. Рассуждения дают вполне определённый результат: предъявляется цепь, которая вполне упорядочена отношением включения и, если множество

содержит больше одного элемента, не совпадает с

. Следовательно,
Ваше предположение, что при

цепь может оказаться единственной, неверно.
Лучше обратите свою придирчивость на свой трактат. Там мест для придирок столько, что работы Вам хватит надолго.
Теорема 1. Существует такое множество

, и существует взаимно однозначное соответствие F между всеми элементами множества

и всеми точками множества

, так что

, где

и

- произвольные элементы множества

, а

и

- точки из

.
Доказательство в основном тесте не приводится, так как теорема тривиальна. Поясняю. Доказательство теоремы 1 можно провести, например, предполагая, что
все множества можно вполнеупорядочить (по процедуре, подобной той, которую применил Кантор для отображения плотного всюду счётного множества в множество рациональных чисел), а можно и без этого предположения,
пользуясь только свойствами I и II, и
аксиомой выбора.
Поскольку возможность вполне упорядочить любое множество равносильна аксиоме выбора, то оба эти способа ничем не отличаются, кроме, возможно, технических деталей, и заведомо предполагают возможность вполне упорядочить каждое множество мощности континуум.
А теорема о существовании линии и есть вывод опровержения вполнеупорядочения континуума. Т.е. в частности из равенства

указанный вывод даёт требуемое.
То есть, Ваше рассуждение внутренне противоречиво:
с одной стороны, Вы нуждаетесь в полном упорядочении континуума (множество

у Вас имеет мощность континуум), а
с другой - отрицаете существование такого упорядочения. На этом, собственно говоря, обсуждение Вашего трактата можно смело закончить, если, конечно, Вы не собираетесь доказывать противоречивость ZFC. Но тогда требования к Вам будут более жёсткими.
И если формальное доказательство Цермело правильно,
Правильно, не сомневайтесь.
Ответьте, пожалуйста,
не уклоняясь, на мой вопрос: Вы действительно считаете всех математиков полными идиотами, не способными за сто лет разобраться в простом рассуждении?
то тем более существует какая-то глубокая ситуация в этом вопросе, до конца пока не прояснённая.
Да прояснённая она, прояснённая. Ваша линия

, которую Вы должны построить, иногда существует, а иногда - нет. Построения этой линии у Вас нет, а то, что Вы выдаёте за построение, таковым не является, поскольку не содержит ничего, кроме пожеланий и неясных образов. Об этом ведь Вам говорят все, кто пытался прочесть Ваш "трактат". На самом деле средствами ZFC такое построение не всегда возможно, и это хорошо известно, поэтому Вы можете до бесконечности повторять заклинание "у меня всё доказано", но никто Вам не поверит.
К тому же, можно сначала не рассматривать моё полное доказательство, т.е. вывод аксиом I-III как теорем, а понять хотя бы аксиомы I, II, III, и выводы из них следующие. Уже они не совместимы с выводом о вполнеупорядочнии,
Это означает, что Ваши аксиомы противоречат ZFC, и надеяться на их доказательство средствами ZFC бессмысленно.
будучи геометрически очевидными.
Я Вам объяснял, что геометрическая очевидность порой обманывает даже в школьных задачах по геометрии, а уж в теории множеств ссылаться на неё совершенно неуместно.
В частности, в одной из аксиом утверждается, что между парой точек можно провести линию, соединяющую эту пару (другое дело, между какой парой).
Это в какой аксиоме у Вас такое утверждается?
Аксиома I. Существует трансформация

, проводимая вдоль дуг

над областью

, в результате которой, концы каждых двух линий

и

, взятых в множестве

, разводятся на дуге

. При этом, если

, то после трансформации (деформации) оказывается:

и

(

- конец линии

,

- конец линии

); трансформированная область

оказывается гомеоморфной открытой евклидовой области.
Эта аксиома сформулирована ужасно, но доказать её, вероятно, можно. Нужно только по-человечески сформулировать. Речь идёт о построении бикомпактного расширения с линейно упорядоченным наростом, в котором линии семейства

будут иметь различные пределы.
Аксиома II. Когда область

приведена в состояние

, для любой точки

, расположенной на дуге

(т.е. на изогнутой гиперпрямой), можно найти линию множества

, имеющую своим концом эту точку

.
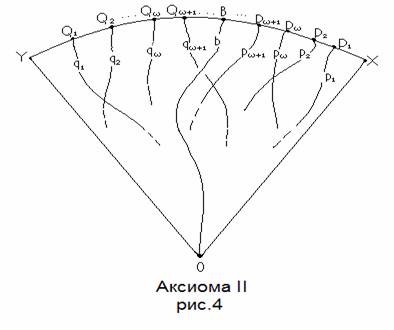
А вот это, как сказал пёс в одном известном мультфильме, "национальная индейская изба - фиг Вам называется". Это не докажете, потому что это неверно. Формулировка, конечно, ужасная, чтобы её понять, надо приложить массу усилий.
Аксиома III. Какова бы ни была мощность множества

, на котором завершён процесс вполне упорядочения, существуют соответствующая этому множеству трансформация

и отрезок

, взятый от некоторой линии плоскости так, что

и

ü

, и

пересекает отрезок

в одной из внутренних точек

. Точка

, лежащая на пересечении отрезков

и

, единственна.
Извините, но это вообще абракадабра какая-то. Я ничего не понял. Скорее всего, то, что Вы имеете в виду, просто неверно, поскольку речь явно идёт о вполне упорядоченном множестве любой мощности.
-- Сб авг 15, 2009 00:41:48 --Ну и понаписали тут. Никак я не успеваю, слишком занят. Поэтому приходится возвращаться к старым сообщениям, про которые все давно забыли.
Я, конечно, понимаю, что Вам хочется избавиться от неудобного оппонента.
Наоборот
Someone, Вы стали задавать наконец вопросы уже технические, которые я и хотел, чтобы мне задавали
Не заблуждайтесь на этот счёт. Я задаю Вам "технические" вопросы исключительно для того, чтобы Вы осознали, что ситуация гораздо сложнее, чем Вам кажется. Технический вопрос о "разведении" линий на границе сектора с моей точки зрения достаточно прост, я Вам
показывал, что для этого не требуются никакие "деформации" и никакие трансфинитные построения, и всё делается в несколько строчек. Проблема не в "разведении концов", а в построении линии

, разделяющей два семейства. Вы всерьёз полагаете, что Ваше "построение"
... Пусть линия

из конфигурации

в каждый момент времени совпадала по положению с одним фиксированным лучом

, и двигалась относительно других линий на растягиваемой вдоль лучей плёнке

, т.е. на той плёнке, по которой двигались и другие элементы конфигурации. Тогда, к моменту

линия

расположится, как покоящаяся линия, среди предельных не движущихся линий конфигураций

в силу того, что лучи пучка

расположатся среди таких линий. Соответственно, линия

в этот момент расположится среди предельных линий конфигурации

, и без ограничений общности можно считать

, если перенести отношения между точками и линиями, и между линиями с сектора

. Используя обратные деформации, находим, что


для момента

. В конфигурации

найдётся линия

, которая переходит в

при отображении

. Меняя индекс

, получаем, что при любом значении индекса, в момент

оказывается

. Аналогично рассуждаем для линии

. В итоге, получаем

при любом

, в конечный момент, ...
действительно является осмысленным? Здесь вообще всё непонятно. Как движутся линии, откуда взялся параметр

, почему "без ограничений общности можно считать"...
shwedka Вам
указала множество моментов, требующих пояснений, явных построений или доказательств.
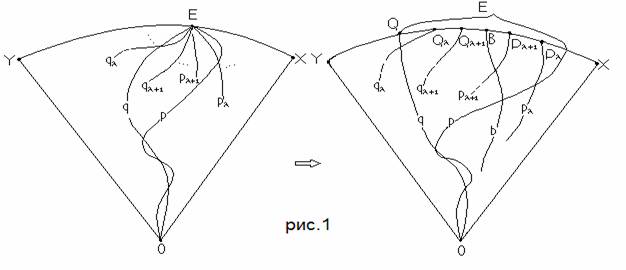
Давайте возьмём конкретное семейство, о котором я говорил ранее:
Аксиома. Пусть
А и
Б – подмножества

, мощность которых меньше или равна

, все элементы объединения этих множеств сравнимы между собой, и каждая линия из
А заканчивается левее каждой линии из
Б. Тогда, существует линия

, которая заканчивается правее каждой линии множества
А и левее каждой линии множества
Б.
Пусть семейство
Б состоит из одной линии

, заданной уравнением

, а семейство
А состоит из линий

, задаваемых уравнениями

,

, причём, если

, то

и

. Предъявите, пожалуйста, линию

. К пятому параграфу своего трактата не отсылайте, продемонстрируйте построение здесь. Постарайтесь изложить попроще. Например, непонятно, зачем нужно использовать трёхмерное пространство, если все линии расположены на куске плоскости. Это только запутывает построение.
Я даже построю семейство
А, чтобы показать, как
должно выглядеть Ваше изложение. Как я понял из Вашего текста и рисунков, Вы отсчитываете угол

от оси

. Так и будем отсчитывать.
Для построения мне понадобятся вспомогательные непрерывные функции

,

,

, которые я определю так:

а при


Заметим, что на каждом отрезке
![$\left[1-\frac 1k,1-\frac 1{k+1}\right]$ $\left[1-\frac 1k,1-\frac 1{k+1}\right]$](https://dxdy-04.korotkov.co.uk/f/f/0/d/f0dd52f9f09d160cc63acedaf55f028882.png)
в точности две из этих функций отличны от

, а именно,

и

, причём, их сумма на этом отрезке равна

. Поэтому, в частности, ряд

сходится на полуинтервале

, и его сумма равна

.
Кроме того, каждая точка

имеет окрестность, в которой отличны от

не более трёх из этих функций (для точки

годится полуинтервал

; если точка принадлежит интервалу

, то годится сам этот интервал; если точка совпадает с

при

,

, то годится

).
Теперь надо построить семейство
А, указанное в приведённой выше цитате из моего
сообщения. Для этого, разумеется, достаточно указать непрерывные функции

,

. Используем построение по индукции по всем ординалам, меньшим

.
Предположим, что для некоторого ординала

уже построены непрерывные функции

,

, удовлетворяющие следующим условиям:
а) для всех

выполняются неравенства

при

, и существует

;
б) если

, то найдётся такое число

, что при всех

выполняется неравенство

.
(Для

множество функций будет пустым.)
Построим

. Рассмотрим три случая.
1) Для

положим

. Заметим, что эта функция непрерывна и

при

, и

, то есть, условие а) выполняется, а условие б) тривиально.
2) Ординал

- не предельный, то есть, существует такой ординал

, что

. Тогда положим

. Эта функция непрерывна, так как по предположению индукции

непрерывна.
Условие а) выполняется:
так как при

по предположению индукции

, то

, то есть,

;
так как

, то

.
Условие б) выполняется:
так как при

выполняется неравенство

, то

;
если задан ординал

, то по предположению индукции найдётся такое число

, что при всех

выполняется неравенство

. Тогда для этого

и

получим

.
3) Ординал

- предельный. Перенумеруем все ординалы, меньшие

, натуральными числами. Таким образом, все ординалы, меньшие

, перечислены в виде последовательности

. Для каждого

и

положим

. Сразу заметим, что эти функции непрерывны на

, и при

выполняются неравенства

.
Определим функцию

. Эта функция непрерывна на

, так как члены этого ряда непрерывны, и для каждой точки рассматриваемого полуинтервала существует окрестность, в которой отличны от

не более трёх членов ряда. Заметим, что при

на отрезке
![$\left[1-\frac 1n,1-\frac 1{n+1}\right]$ $\left[1-\frac 1n,1-\frac 1{n+1}\right]$](https://dxdy-03.korotkov.co.uk/f/2/3/4/234097ca7b29823468fc0b0115fbf61a82.png)
выполняются неравенства
то есть,

. Поскольку

можно взять произвольным, неравенство

выполняется при всех

.
Наконец, положим

. Эта функция непрерывна. Проверим, что выполняются условия а) и б).
Условие а):
так как при

имеем

, то

, то есть,

;
так как

и

при

, то, по теореме о двух милиционерах,

, откуда

.
Условие б):
пусть

; существует такое

, что

. Тогда при

из неравенства

получаем

, то есть,

при

.
Таким образом, требуемая функция

построена, и можно продолжать построение дальше.
Требуемое семейство
А, таким образом, построено.
Теперь Ваша задача состоит в том, чтобы построить линию

, разделяющую семейства
А и
Б. Построение должно быть в таком стиле, как я продемонстрировал: никаких неопределённых элементов и недоказанных свойств быть не должно.
Возьмётесь?P.S. Академик П.С.Александров говорил как-то на семинаре: "Соискатель обычно тратит очень много усилий, чтобы сделать первую ошибку. Потом результаты начинают сыпаться, как из рога изобилия."
Мне кажется, что Вам много усилий тратить не пришлось. Но последствия те же: эпохальные результаты сыплются действительно как из рога изобилия.