Попробую реанимировать тему.
Ищу желающих поучаствовать в распределенном вычислении.
Цель - найти 15 последовательных чисел, имеющих в точности по 12 делителей.
Легко показать, что для каждого натурального

найдется

- длина максимальной цепочки последовательных натуральных чисел, имеющих в точности по

натуральных делителей.
Для нечетных


всегда равно 1. С четными все гораздо интереснее. На сегодняшний день известно несколько сотен

,
для которых найдено точное значение

. Но во всех этих случаях

.
Из значений, больших 7, наиболее реально найти

. Известно, что

. У меня есть код (на PARI) для поиска цепочки из 15 чисел.
Но прикидка показывает, что на моем (довольно быстром) компе на это потребуется лет 7-10.
Но если навалиться коллективно, процесс ускорится.
Я запускаю сразу несколько экземпляров PARI. Каждый задействует одно логическое ядро процессора и совсем немного памяти. При этом ничего не тормозит. Перезапускаю вручную сразу все процессы одновременно. Дней на 5, чтобы не тратить время (минут 10) на перезапуск часто.
Ищу сообщников. Обращайтесь. Пришлю код и пояснения. (PAPI ставится на комп за несколько минут.)
====================================
6 апреля 2022 года цепочка из 15 последовательных чисел, имеющих по 12 делителей была найдена Дмитрием Петуховым!
Но поиск

для других

продолжается.
Здесь будут обновляться таблицы, связанные с задачей отыскания

для четных

Цепочки, для которых

, возможны только для

, кратных 12.
На данный момент такие цепочки известны для перечисленных ниже значений:
12,
24,
36,
48,
60,
72,
84,
96,
108,
120,
132,
144,
156,
168,
180,
192,
204,
216,
228,
240,
252,
264,
288,
300,
312,
324,
336,
360,
384,
396,
408,
420,
432,
456,
468,
480,
504,
528,
540,
552,
576,
588,
600,
624,
648,
660,
672,
720,
756,
768,
792,
816,
840,
864,
900,
936,
960,
972,
1008,
1080,
1176,
1200,
1260,
1296,
1320,
1500,
1512,
1584,
1620,
1680,
1800,
1848,
1872,
1944,
2160,
2268,
2520,
3000,
3240,
3600,
3888,
4536,
5040,
5832,
6480,
7128,
9720,
11664.
При этом максимальная длина известной на сегодняшний день цепочки равна 8 для следующих значений

:
Код:
204, 228, 396, 408, 420, 456, 468, 552, 588, 624, 660, 672, 756, 816, 840, 864, 900, 936, 972, 1008, 1176, 1200, 1260, 1320, 1500, 1512, 1584, 1620, 1680, 1800, 1848, 1872,
1944, 2268, 2520, 3000, 3240, 3600, 3888, 4536, 5040, 5832, 6480, 7128, 9720, 11664
Цепочки длиной 9 известны для следующих

:
Код:
132, 156, 180, 252, 264, 300, 312, 324, 504, 528, 540, 600, 720, 768, 792, 1080, 1296, 2160
Цепочки длиной 10 найдены для следующих

:
Код:
84, 108, 336, 432, 480, 576, 648, 960
Цепочки длиной 11 удалось найти для следующих

:
Код:
60, 168, 288, 360
А цепочки длиной 12 для
Код:
120, 216, 240, 384
Приведенная ниже таблица содержит сведения о самых длинных цепочках для тех

, для которых

.

- длина самой длинной известной на сегодняшний день цепочки для данного

(Lower bound);

- доказанная оценка сверху для максимальной длины цепочки для данного

(Upper bound).
Таким образом

Цепочки, найденные Евгением Жилицким и Артёмом Заржецким (и Дмитрием Петуховым

), получены с помощью программ Дмитрия Петухова.
Приводимые ниже (не только в таблице, но и после нее) оценки

сверху получили и улучшили Ivo Düntsch, Roger B. Eggleton, Hugo van der Sanden, Василий Дзюбенко, Владимир Лецко,
Евгений Жилицкий и Денис Шатров.
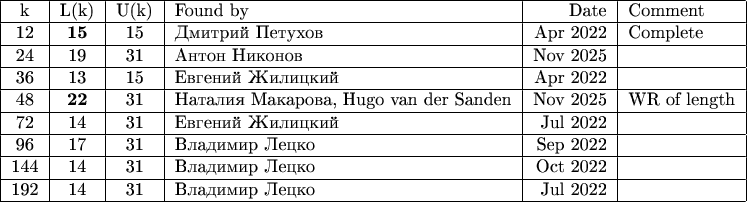
Рекордная по длине цепочка открывается числом 91961526307286709380597649336434597932204049205291537.
Если

, то

. Ниже перечислены все

указанного вида, для которых известны цепочки длины 7:
Код:
8, 16, 20, 28, 32, 40, 44, 52, 56 , 64, 68, 76, 80, 88, 92, 100, 104, 112, 116, 124, 128, 136, 140, 148, 152, 160, 164, 172,
176, 184, 188, 196, 200, 208, 220, 224, 232, 248, 256, 260, 272, 280, 296, 308, 320, 340, 352, 364, 380, 392, 400, 416, 440,
448, 476, 484, 500, 512, 560, 640, 700, 704, 784, 800, 896, 1000, 1024, 1120, 1280, 1600, 1792, 2000*, 2048, 2500*, 2560, 4096.
Денис Шатров доказал, что, для всех

вида

справедлива оценка

.
Вот список значений

, для которых известны цепочки длины 5:
Код:
6, 18, 30, 42, 54, 66, 78, 90, 102, 114, 126, 138, 150, 162, 174, 186, 198, 210, 222, 234, 246, 258, 270, 282, 294, 306, 318,
330, 342, 354, 366, 378, 390, 414, 426, 438, 450, 462, 474, 486, 498, 510, 522, 546, 558, 570, 594, 630, 666, 690, 702, 714,
726, 750, 798, 810, 858, 870, 882, 918, 930, 966, 990, 1014, 1050, 1122, 1134, 1170, 1218, 1242, 1254, 1326, 1350, 1386, 1458,
1470, 1482, 1518, 1530,1554, 1638, 1650, 1710, 1734, 1782, 1794, 1890, 1914, 1938, 1950, 2046, 2058, 2106, 2142, 2166, 2178,
2250, 2310, 2394, 2430, 2550, 2574, 2646, 2730, 2754, 2850, 2970, 3150, 3402, 4374, 5670, 6750, 7290, 9450, 10206, 12150,
13122, 17010, 20250, 21870.
Скорее всего, для всех

, сравнимых с

по модулю 12 (за исключением
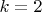
)

.
Оценку

для таких

удалось строго доказать для следующих случаев:

, где

- простое число, большее 3;

, где

- простые числа, большие 3 (не обязательно различные);

, где

, а

- простые числа такие, что

.
Последнее условие позволяет искать подходящие тройки даже для очень больших

.
Например, для

(это больше триллиона!) поиск соответствующей тройки занял несколько минут.
В прилагаемой таблице представлены числа, открывающие цепочки последовательных чисел, имеющих по

делителей, для всех таких

(кроме помеченных звездочкой: они попадут в обновленную версию), для которых такие цепочки известны и

.
А
здесь представлены результаты работы команды, занимающейся поиском минимальных цепочек с 12 делителями.