Код:
[7.350000, 22.64000, 29.67000, 23.38000, 11.93000, 3.840000, 1.190000]
Здесь слева направо процент:
более 6-и простых. Это статистика для цепочек длины 10. Соответственно числа 30-значные
Асимптотическая формула для количества

-почти простых чисел

, при фиксированном

:
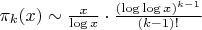
показывает, что поведение

как функции от

(при фиксированном большом

) имеет максимум. А именно, отношение последовательных значений:
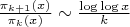
Таким образом:
- Если
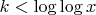
, то отношение больше 1, и

возрастает с ростом

.
- Если
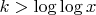
, то отношение меньше 1, и

убывает с ростом

.
Максимум достигается при
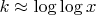
, что согласуется с теоремой Харди-Рамануджана о среднем количестве простых делителей числа.
Поэтому при фиксированном

количество

-почти простых чисел сначала возрастает с ростом

, достигает максимума при
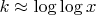
, а затем убывает.
Ниже приведена таблица для

от

до

, где вычислено
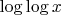
и определено
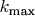
— значение

, максимизирующее

.
|

|
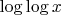
(приблизительно) |
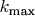
|
|-------------|----------------------------------|-------------------|
|

| 3.14 | 4 |
|

| 3.83 | 4 |
|

| 4.24 | 5 |
|

| 4.52 | 5 |
|

| 4.75 | 5 |
|

| 4.93 | 5 |
|

| 5.08 | 6 |
|

| 5.22 | 6 |
|

| 5.33 | 6 |
|

| 5.44 | 6 |
Эта таблица показывает, что распределение

-почти простых чисел имеет колоколообразную форму с максимумом, сдвигающимся вправо с увеличением

.
Для

рассмотрим относительную долю

— нормированную плотность, которая показывает вклад каждого

в общее количество

-почти простых чисел.
Для этого вычисляем
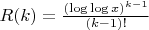
для

от 1 до 15, затем нормируем так, чтобы сумма
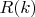
равнялась 1.
Таблица плотностей

для

|

|
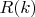
|

(нормированная) |
|-------|----------|--------------------------|
| 1 | 1.000 | 0.00435 |
| 2 | 5.438 | 0.02368 |
| 3 | 14.785 | 0.06438 |
| 4 | 26.800 | 0.1167 |
| 5 | 36.425 | 0.1586 |
| 6 | 39.608 | 0.1725 |
| 7 | 35.890 | 0.1563 |
| 8 | 27.880 | 0.1214 |
| 9 | 18.940 | 0.0825 |
| 10 | 11.440 | 0.0498 |
| 11 | 6.220 | 0.0271 |
| 12 | 3.076 | 0.0134 |
| 13 | 1.394 | 0.00607 |
| 14 | 0.583 | 0.00254 |
| 15 | 0.226 | 0.000984 |
Распределение напоминает распределение Пуассона с параметром
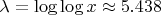
. Распределение имеет длинный хвост справа.