А полностью стационарных не нижних по энергии состояний возможно вообще нигде нет.
Тогда и нас всех тоже нет. Попытка повернуть тему от философии к физике. К черту водород, с ним сложно. Пусть двухуровневая система находится в классическом электромагнитном поле и может излучать фотон в единственную моду идеального резонатора бесконечной добротности. Гамильтониан в приближении Джейнса-Каммингса:
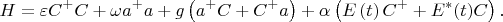
Все энергии и частоты отсчитываются от энергии основного состояния.

- фермионный оператор уничтожения состояния в двухуровневой системе,

- аналогичный бозонный оператор для фотона.
Волновая функция
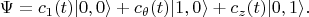
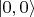
- основное состояние;
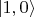
- возбужденное состояние атома, фотонов нет;
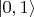
- один фотон, атом в основном состоянии.
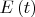
- внешнее классическое возбуждающее поле. Все решается точно. Пусть система в начальный момент сидит в основном состоянии, классическое поле действует короткое время (начиная с

внешнего поля нет) и выключается. Возможный ответ:
Вложение:
e1.png
После выключения поля получается то самое смешанное состояние основного и возбужденного состояния атома
и фотона (на графике

вероятность (квадрат модуля

) найти систему в основном состоянии, и далее - аналогично. Получается то самое смешанное состояние атома +
фотон. Если я попытаюсь измерить наличие фотона в резонаторе, то с вероятностью 0.4 я его найду. При этом "атом" окажется в основном состоянии. Если разрешить фотону улетать из резонатора, а "атому" спонтанно излучать, то атом в конце концов окажется в основном состоянии, а фотон улетит далеко-далеко, причем не один. При этом улетает разное "количество" фотонов с разной вероятностью. Вот и вся проблема.