Может я чего-то не понимаю, ну так объясните.
Объяснил бы, если бы на форумах имелась такая же возможность последовательно, "с нуля", излагать КМ, с выкладками, как в вузовском преподавании: с лекциями, с упражнениями по решению задач, с требованием изучать литературу, и главное - с научной практикой в лабораториях. И если бы собеседники (в том числе и я :) были бы мотивированы к тому, чтобы так напрягаться, и имели бы для этого время. А когда это всерьёз никому не надо, то и объяснять толком не получится.
первое, что я замечаю в ваших суждениях здесь - это недоверие к экспериментальной физике. Например, вот это ваше утверждение ошибочно:
По-моему, в реальности начальное состояние полей (и не только электромагнитного) определить с достаточной точностью невозможно никогда.
С
математической точностью да, невозможно определить. Но КМ это не абстрактная математика, а физическая теория - теснейшим образом связанная с реальными экспериментами. Физики в опытах как раз с
достаточной точностью контролируют состояния известных полей и выявляют все факторы, существенно влияющие на результаты измерений. C достаточной для того, чтобы в KM-теории удавалось учитывать именно основные факторы, а на разброс из-за погрешностей измерений уже не обращать внимания.
Единственное из предположительно существенного, что не могут контролировать экспериментаторы, это - гипотетические скрытые параметры, если они в природе есть. Если Вы скажете о себе: "я верю, что теория, более фундаментальная чем КМ, это какая-то теория со скрытыми параметрами (ТСП)", то я не стану возражать. Но когда Вы говорите
В реальности нам в лучшем случае будет известно только то, что в нулевой момент электрон находится в суперпозиции между 1s и 2p орбиталями, а про поле вообще неизвестно почти ничего
то допускаете ошибку: Вы игнорируете экспериментальные факты и сопутствующую им КМ-теорию.
Вот факты:
Изучение спектров атомов показывает, что ширины спектральных линий зависят от ряда факторов. Есть столкновительное уширение (из-за соударений атомов в газе друг с другом, оно зависит от концентрации), есть допплеровское уширение (из-за теплового движения атомов, оно зависит от температуры), и есть "естественная ширина линий" - неустранимая даже в случае самых разреженных и холодных газов.
КМ позволяет вычислить естественные ширины линий для конкретных атомов и конкретных их линий как
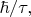
где

- средние "времена жизни" атомов в различных состояниях. Значения

получаются не бесконечными из-за не равной нулю вычисляемой теоретически вероятности
спонтанных переходов атомов из возбуждённых состояний в нижние по энергии. Термин "спонтанный переход" означает, что ЭМ-поле в окружающем пространстве в начальном состоянии задаётся при вычислениях как не возбуждённое: ноль фотонов во всех модах поля.
Оказывается, вычисленные так ширины линий неплохо совпадают с измеренными в опытах естественными ширинами линий. Измерения делали разные группы физиков в разных условиях (разные толщины стен и крыш зданий, разное оборудование, время суток разное, времена года разные, и сами годы разные. Не обнаружено влияния посторонних переменных факторов - как локальных, так и удалённого от нас положения планет, Солнца, галактик и всего остального во вселенной.
Подобное согласие КМ-расчётов, основанных на отсутствии возбуждений внешнего поля в начальном состоянии, с результатами измерений означает, что спонтанный распад возбуждённых состояний атомов не объяснить присутствием неучтённых полей.
Получается, причина стохастичности (т.е. в общем случае отсутствие детерминированности в поведении квантового объекта) находится вне сферы применимости понятий КМ. Если эта причина и будет найдена, то не в КМ, а в какой-то ещё не созданной будущей теории (в ТСП или в более хитрой). Выполненные к настоящему времени эксперименты не указывают, как и где искать такую причину.
Второй бросающийся в глаза недостаток ваших суждений - отсутствие количественного анализа в обсуждении КМ, и, как следствие, необоснованность утверждений. Пример:
Если реально "экранировать" атом водорода, то мы получим не задачу на атом водорода в пустом пространстве, а задачу на атом водорода в резонаторе. Что совсем не то же самое и динамика его будет, очевидно, совсем иной.
А
насколько иной будет динамика? Как результат зависит от линейного размера

или от объёма

"ящика", в котором определяются моды поля?
Вот ответ:
В ящике квантования (он же - "нормировочный объём") размером

спектр волновых векторов, нумерующих моды поля, дискретен; интервалы между соседними разрешёнными значениями проекций волнового вектора равны
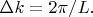
Пусть

будет порядка метра (порядок размера лабораторного стола); можно и больше взять -

порядка размеров лаборатории в помещении с толстыми стенами, играющими роль экранировки. Фотонам, которые излучаются или поглощаются атомами в оптическом диапазоне частот, соответствуют длины волн (это доли микрона)
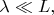
т.е. величины волновых векторов
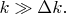
Т.е. в таких задачах спектр мод поля настолько густой, что в практическом плане не отличим от непрерывного спектра в пространстве неограниченных размеров. Поэтому влияние корпуса установки или стен лаборатрии на поведение изучаемых атомов внутри установки в таком случае пренебрежимо мало. Экспериментаторы это знают, они же не идиоты, чтобы прозевать подобное влияние, если бы оно было заметным. Их работа в том и заключается: всё замечать, и всё проверять - что на что и как влияет. И теоретические КМ-расчёты тоже так делаются. Ведь физики-теоретики тоже не идиоты. Они выяснили, что промежуточные выкладки удобно выполнять, считая нормировочный объём

произвольно большим, но конечным: в выкладках бывает удобнее работать с дискретным спектром, чем с непрерывным. Поскольку результат расчёта, сопоставимый с экспериментом, не должен зависеть от произвольного нормировочного объёма, такой результат допускает переход к пределу
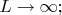
так и поступают, и такие результаты КМ-теории успешно согласуются с данными опытов.
А даже если взять задачу об атоме в резонаторе малых размеров (пример есть в отделившейся отсюда теме), что в ней плохого? Чем она не годится для аналогичных раздумий о природе вероятностей в квантовой физике? Ещё и лучше годится - расчёт там более простой, а результат тоже статистический, и тоже демонстрирует спонтанные переходы атома (уже
после выключения возбуждающего поля) из возбуждённого состояния при нуле фотонов в резонаторе, начинающиеся в те моменты времени, когда вероятность атому быть в возбуждённом состоянии максимальна. Динамика вероятностей в этой задаче ещё и интереснее - периодически повторяющаяся (осцилляции Раби).
В третьих, почему Вы ограничиваетесь в своих рассуждениях только картиной излучения атомом фотона? Есть же много других задач в КМ, (притом разных!), в которых вопрос о природе вероятностей выглядит не менее, а даже более острым.
Вот простая задачка из учебного курса для студентов - о зависимости от энергии

вероятностей надбарьерного отражения и прохождения частицы с массой

. Оказывается, частица почти при всех значениях энергии с некоторой вероятностью отражается, а с некоторой вероятностью проходит за прямоугольный потенциальный барьер с конечной длиной

Если же энергия её такова, что на длине

укладывается целое число половин дебройлевских длин волн

частицы (
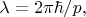
где

- импульс частицы над барьером:
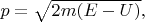

- высота барьера на шкале энергии), то вероятность отражения обращается в ноль. Частица с такой энергией проходит за такой барьер с достоверностью! Почему тут исчезает стохастичность поведения частицы? При так выбранных значениях
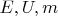
и

исчезают "неопределённые поля во вселенной" и "скрытые параметры"? :)
КМ овечает на это просто: если амплитуды вероятностей отразиться ближним или дальним краем барьера оказываются противофазными, то их сумма обращается в ноль (деструктивная интерференция амплитуд вероятности); и поэтому частица перестаёт отражаться. Это один из примеров того, что я называю интерференционным характером распределения вероятностей. Для фотонов есть аналогичный эффект при отражении от двух границ сред с различающимися показателями преломления; он применяется на практике для изготовления "просветлённой" оптики. Другой пример интерференции амплитуд вероятностей - знаменитый "двухщелевой эксперимент".
Вот ещё пример, важный для практики и, кстати, подходящий для изложения принципов КМ начинающим ученикам - дифракция частиц (рентгеновских фотонов, нейтронов, электронов) на кристаллических решётках. Тут наряду с тем, что каждая очередная частица при упругом рассеянии на кристалле попадает на детектирующем экране
случайным образом в тот или иной "рефлекс" (яркое "пятно"), она почти никогда не попадает в тёмные области между рефлексами. И картина эта
контролируемо изменяется при повороте кристалла и изменении импульса частиц. Притом она зависит от выбора кристалла; как раз в таких опытах выявлялись детали кристаллической структуры различных веществ. Такое поведение, чётко управляемое локальной настройкой эксперимента, не объяснить какой-то "неопределённостью поля во вселенной".
В этой ветке (про интерпретацию КМ) есть ещё неверные утверждения о КМ, обусловленные, очевидно, недостатоком у пишущих знания предмета. Например, будто "процесс измерений описывает КЭД. И в КЭД никаких классических приборов нет."
КТП, и в частности КЭД, это обобщение принципов КМ с механических систем с конечным числом степеней свободы на системы с бесконечным числом степеней свободы - поля. Те же принципы, только формализм получается намного более сложный.
Пункт о классичности приборов вообще следовало бы разъяснить подробно, но у меня сообщение вышло уже очень длинным, поэтому пока лишь кратко скажу: классические приборы - это основное феноменологическое понятие в КМ, наряду с классическими представлениями о симметриях физического пространства и о движении тел в нём. Все базисные векторы состояний в формализме КМ служат для описания классических приборов в контексте квантовых опытов. (Но это выясняется, разумеется, не наспех, а при последовательном построении формализма КМ на основе рассмотрения разных экспериментов).
Поэтому не нужно добавлять в КМ ещё раз описание приборов - типа измерения приборов сверхприборами, как это безуспешно пытается делать до сих пор так и не созданная "теория измерений" (если, конечно, не считать "успехом" оторванную от реального опыта ерунду про бесчисленную кучу ненаблюдаемых вселенных :). И не нужно из "теории измерений" пытаться выводить классическую механику. Классические приборы и классическая механика (с определением физических величин через принцип соответствия) уже заложены в КМ, - вместе с феноменологическим описанием стохастичности, глубинное происхождение которой остаётся загадочным.
Большинство учёных, занятых практической квантовой физикой, всё это прекрасно понимают. Вы никогда не услышите в лабораториях слов типа "хм... странный коллапс наблюдаю, по-копенгагенски не понять, может попробовать решить данную задачу по Бому, или по Крамеру, или по ММИ?" И не услышите в лабораториях: "хм..., где же у нас тут прошёл Hesenberg cut?" Есть долгоживущий (причины живучести понятны, их можно обсудить отдельно) около-квантово-механический математико-философский то ли литературный жанр, то ли квазинаучная пиар-тусовка с успешным привлечением внимания СМИ: "интерпретации КМ" называется. Вот там подобные вопросы и муссируются.