realeugene, да, в глобальном времени. Впрочем, как я понимаю, точки делимости вообще образуются только в нерелятивистском приближении, то есть когда размеры системы малы и временем распространения света через систему можно пренебречь. Совмещается это всё примерно так же как в бомовской механике или как в том же клеточном автомате 'т Хоофта: на фундаментальном уровне лоренц-инвариантности нет, но фундаментальный уровень скрыт от прямого наблюдения. Впрочем, этот вопрос ещё требует изучения, и я думаю автор рассмотрит его в будущих работах. Пока есть только доказательство причинной локальности теории, то есть невозможности причинного влияния простраственно-удалённых частей системы друг на друга. Но это в отдельной работе, её я детально пока не изучал, так по диагонали просмотрел.
-- 12.08.2025, 02:07 --Утундрий, краткий пересказ такой.
Пусть есть некоторая система, которая в каждый момент времени может пребывать в одном из

состояний (обобщение на непрерывный набор состояний прямолинейное, в этом пересказе я ограничусь дискретным случаем). И пусть есть набор вероятностей
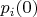
,

,
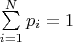
, и известно, что в момент времени

система с вероятностью
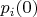
пребывает в

-м состоянии. Природа вероятностей может быть любая обычная: частотности в воображаемом или реальном анасабле, байесовская степень уверенности и др. Динамика системы задана в виде
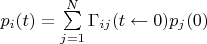
, где

— вероятность нахождения системы в

-м состоянии в произвольный момент

, а
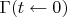
—
стохастическая матрица, то есть матрица c неотрицательными элементами, все колонки которой суммируются в единицу.
Такая система называется обобщённой стохастической системой. Оказывается, она обладает рядом замечательных свойств.
Во-первых, матрицу
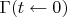
без ограничения общности можно считать
унистохастической, то есть
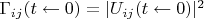
, где
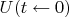
— унитарная (комплексная) матрица.
Во-вторых, в общем случае не существует стохастической матрицы
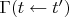
такой, что
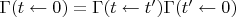
. Моменты времени

для которых это всё-таки выполняется (для
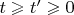
) называются точками делимости.
В-третьих, если рассмотреть систему из двух определённым образом взаимодействующий подсистем, где вторая часть — среда с большой информационной ёмкостью (декогеренция), то оказывается, что для первой подсистемы постоянно формируются точки делимости и система в целом ведёт себя как обычная классическая система с марковским свойством. (Тут на самом деле есть проблемка: формулы-то получаются вроде бы какие надо, но они не гарантируют на самом деле "классичности" поведения.)
В-четвёртых, в такой системе наблюдаются типичные квантовые эффекты: интерференция и запутанность. Причём это больше чем просто аналогия, это точное математическое соответствие.
Вот вкратце как-то так.