Сонантометрия или алгебра музыкальной гармонии.

[commator]

Для ясности отображено множество, составленное как последовательность во времени нескольких вертикальных схем обычной $\mbox{12РДО\vee}\mathrm{12EDO}$ клавиатуры, где не нажатые черные и белые клавиши показаны квадратиками соответствующих цветов:

$ \left\{\begin{matrix} : &: &: &: &: &: &: &: \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{D\natural{\pm}0}{\underset{0,5873}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{D\flat{\vee}C\sharp{\pm}0}{\underset{0,5544}{\mathsf{\blacksquare}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{C\natural{\pm}0}{\underset{0,5233}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{B\natural{\pm}0}{\underset{0,4939}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{B\flat{\vee}A\sharp{\pm}0}{\underset{0,4662}{\mathsf{\blacksquare}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{B\flat{\vee}A\sharp{\pm}0}{\underset{0,4153}{\mathsf{\blacksquare}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{G\natural{\pm}0}{\underset{0,3920}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{G\flat{\vee}F\sharp{\pm}0}{\underset{0,3700}{\mathsf{\blacksquare}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{F\natural{\pm}0}{\underset{0,3492}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{E\natural{\pm}0}{\underset{0,3296}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{E\flat{\vee}D\sharp{\pm}0}{\underset{0,3111}{\mathsf{\blacksquare}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{D\natural{\pm}0}{\underset{0,2937}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{D\flat{\vee}C\sharp{\pm}0}{\underset{0,2772}{\mathsf{\blacksquare}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{C\natural{\pm}0}{\underset{0,2616}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{B\natural{\pm}0}{\underset{0,2469}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{B\flat{\vee}A\sharp{\pm}0}{\underset{0,2331}{\mathsf{\blacksquare}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{A\natural{\pm}0}{\underset{0,2200}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{A\flat{\vee}G\sharp{\pm}0}{\underset{0,2077}{\mathsf{\blacksquare}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{G\natural{\pm}0}{\underset{0,1960}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{G\flat{\vee}F\sharp{\pm}0}{\underset{0,1850}{\mathsf{\blacksquare}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{F\natural{\pm}0}{\underset{0,1746}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{E\natural{\pm}0}{\underset{0,1648}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{E\flat{\vee}D\sharp{\pm}0}{\underset{0,1556}{\mathsf{\blacksquare}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\scriptstyle\overset{D\natural{\pm}0}{\underset{0,1468}{\mathsf{\square}}} &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square \\ : &: &: &: &: &: &: &: \end{matrix}\right. \left.\begin{matrix} : &: &: &: &.\cdot \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{D\natural{\pm}0}{\underset{0,5873}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\overset{D\flat{\vee}C\sharp{\pm}0}{\underset{0,5544}{\mathsf{\blacksquare}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{C\natural{\pm}0}{\underset{0,5233}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{B\natural{\pm}0}{\underset{0,4939}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\overset{B\flat{\vee}A\sharp{\pm}0}{\underset{0,4662}{\mathsf{\blacksquare}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\overset{A\flat{\vee}G\sharp{\pm}0}{\underset{0,4153}{\mathsf{\blacksquare}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{G\natural{\pm}0}{\underset{0,3920}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\overset{G\flat{\vee}F\sharp{\pm}0}{\underset{0,3700}{\mathsf{\blacksquare}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{F\natural{\pm}0}{\underset{0,3492}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{E\natural{\pm}0}{\underset{0,3296}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\overset{E\flat{\vee}D\sharp{\pm}0}{\underset{0,3111}{\mathsf{\blacksquare}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{D\natural{\pm}0}{\underset{0,2937}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\overset{D\flat{\vee}C\sharp{\pm}0}{\underset{0,2772}{\mathsf{\blacksquare}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{C\natural{\pm}0}{\underset{0,2616}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{B\natural{\pm}0}{\underset{0,2469}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\overset{B\flat{\vee}A\sharp{\pm}0}{\underset{0,2331}{\mathsf{\blacksquare}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{A\natural{\pm}0}{\underset{0,2200}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\overset{A\flat{\vee}G\sharp{\pm}0}{\underset{0,2077}{\mathsf{\blacksquare}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{G\natural{\pm}0}{\underset{0,1960}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\overset{G\flat{\vee}F\sharp{\pm}0}{\underset{0,1850}{\mathsf{\blacksquare}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{F\natural{\pm}0}{\underset{0,1746}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{E\natural{\pm}0}{\underset{0,1648}{\mathsf{\square}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\overset{E\flat{\vee}D\sharp{\pm}0}{\underset{0,1556}{\mathsf{\blacksquare}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\square &\color[rgb]{.6,.6,.6}\scriptstyle\overset{D\natural{\pm}0}{\underset{0,1468}{\mathsf{\square}}} &.. \\ : &: &: &: &\cdot. \end{matrix}\right\} $

Надпись над квадратиком — энгармоническая фикта — выражает принадлежность со́звука клавиши к высотному классу указанного имени с поправкой $\mbox{12РДО\vee}\mathrm{12EDO}$ высоты этого имени на указанное количество центов. Под квадратиком — частота стимула в килогерцах, дающая ощущение высоты нажатой клавиши с учётом её поправки на энгармоническую фикту.

Нажатие клавиши призвана символизировать замена квадратика на сонантометрическую формулу со́звука, попадающего в категорию высот, этой клавиши.

[commator]

commator в сообщении #1166766 писал(а):

Нажатие клавиши призвана символизировать замена квадратика на сонантометрическую формулу со́звука, попадающего в категорию высот, этой клавиши.

commator в сообщении #1166363 писал(а):

commator в сообщении #1166324 писал(а):

начальный фрагмент всех сочетаний $\mbox{:S}_m\mbox{s}_n$ в системе $\mbox{ЧИП23}\vee\mbox{JIL23}$

$ \left\{\begin{matrix} : &: &: &: &: &: &: &: \\ \scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{2d\mathsf{{:}T\o}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}2Tt}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TDd}}} &\scriptstyle\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}3T2t}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TMm}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}2TDdt}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TQq}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}4T3t}}} \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{C\sharp{-}30}{\underset{0,5448}{\mathsf{{:}Rq}}} &\scriptstyle\overset{C\sharp{-}14}{\underset{0,5500}{\mathsf{{:}DM3t}}} \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{C\natural{-}33}{\underset{0,5133}{2c\mathsf{{:}Q2t}}} &\scriptstyle\overset{C\natural{+}16}{\underset{0,5280}{\mathsf{{:}2Dm}}} &\scriptstyle\overset{C\natural{+}47}{\underset{0,5378}{\mathsf{{:}Ndt}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{C\natural{-}33}{\underset{0,5133}{\mathsf{{:}TQ3t}}} \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{B\natural{-}18}{\underset{0,4889}{1b\mathsf{{:}Md}}} &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}TMdt}}} &\scriptstyle\overset{B\natural{+}31}{\underset{0,5029}{\mathsf{{:}2TDq}}} &\scriptstyle\overset{B\natural{-}61}{\underset{0,4767}{\mathsf{{:}R3t}}} \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{B\flat{+}12}{\underset{0,4693}{\mathsf{{:}3Tm}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{1a\mathsf{{:}Dt}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}TD2t}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}2Ddt}}} &\scriptstyle\overset{A\natural{+}81}{\underset{0,4610}{\mathsf{{:}Nq}}} &\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}2TD3t}}} \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{A\flat{-}19}{\underset{0,4107}{\mathsf{{:}Qm}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{G\sharp{+}16}{\underset{0,4190}{\mathsf{{:}TMq}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{G\natural{-}4}{\underset{0,3911}{1g\mathsf{{:}2Td}}} &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}3Tdt}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{G\natural{+}49}{\underset{0,4033}{\mathsf{{:}N3t}}} \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{F\sharp{-}16}{\underset{0,3667}{1f\mathsf{{:}M2t}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{F\sharp{+}33}{\underset{0,3771}{\mathsf{{:}2Dq}}} &\scriptstyle\overset{F\sharp{-}16}{\underset{0,3667}{\mathsf{{:}TM3t}}} \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{F\natural{+}14}{\underset{0,3520}{\mathsf{{:}TDm}}} &\scriptstyle\overset{F\natural{-}35}{\underset{0,3422}{\mathsf{{:}Qdt}}} &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{E\natural{+}29}{\underset{0,3352}{1e\mathsf{{:}3Tq}}} &\scriptstyle\overset{E\natural{+}2}{\underset{0,3300}{\mathsf{{:}2D3t}}} \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{1d\mathsf{{:}\O\o}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Tt}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Dd}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}2T2t}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Mm}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}TDdt}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Qq}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}3T3t}}} \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{C\natural{-}33}{\underset{0,2567}{1c\mathsf{{:}Q3t}}} \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{B\natural{-}18}{\underset{0,2444}{\mathsf{{:}Mdt}}} &\scriptstyle\overset{B\natural{+}31}{\underset{0,2514}{\mathsf{{:}TDq}}} &\color[rgb]{.6,.6,.6}\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{B\flat{+}12}{\underset{0,2347}{b\mathsf{{:}2Tm}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{A\natural{\pm}0}{\underset{0,2200}{a\mathsf{{:}D2t}}} &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{A\natural{\pm}0}{\underset{0,2200}{\mathsf{{:}TD3t}}} \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{G\sharp{+}16}{\underset{0,2095}{\mathsf{{:}Mq}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{G\natural{-}4}{\underset{0,1956}{g\mathsf{{:}Td}}} &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}2Tdt}}} &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{F\sharp{-}16}{\underset{0,1833}{\mathsf{{:}M3t}}} \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{F\natural{+}14}{\underset{0,1760}{f\mathsf{{:}Dm}}} &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{E\natural{+}29}{\underset{0,1676}{e\mathsf{{:}2Tq}}} &\color[rgb]{.6,.6,.6}\square \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare \\ \color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{d\mathsf{{:}\O t}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}T2t}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}Ddt}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}2T3t}}} \\ : &: &: &: &: &: &: &: \end{matrix}\right. \left.\begin{matrix} : &: &: &: &.\cdot \\ \scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}T2D2d}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}2TMmt}}} &\scriptstyle\overset{D\natural{-}82}{\underset{0,5600}{\mathsf{{:}DQn}}} \scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TNn}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}3TDd2t}}} &.. \\ \scriptstyle\overset{C\sharp{-}1}{\underset{0,5541}{\mathsf{{:}P2d}}} &\scriptstyle\overset{D\flat{+}9}{\underset{0,5573}{\mathsf{{:}Umt}}} &\scriptstyle\overset{C\sharp{-}67}{\underset{0,5333}{\mathsf{{:}2TMn}}} &\scriptstyle\overset{C\sharp{+}24}{\underset{0,5622}{\mathsf{{:}Vd2t}}} &.. \\ \scriptstyle\overset{C\natural{-}6}{\underset{0,5215}{\mathsf{{:}4T2d}}} &\scriptstyle\overset{C\natural{+}16}{\underset{0,5280}{\mathsf{{:}T2Dmt}}} &\scriptstyle\overset{C\natural{-}56}{\underset{0,5067}{\mathsf{{:}Un}}} &\scriptstyle\overset{C\natural{-}33}{\underset{0,5133}{\mathsf{{:}DQd2t}}} \scriptstyle\overset{C\natural{+}47}{\underset{0,5378}{\mathsf{{:}TNd2t}}} &.. \\ \scriptstyle\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}DM2d}}} &\scriptstyle\overset{B\natural{+}17}{\underset{0,4987}{\mathsf{{:}Pmt}}} &\scriptstyle\overset{B\natural{-}49}{\underset{0,4800}{\mathsf{{:}T2Du}}} &\scriptstyle\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}2TMd2t}}} &.. \\ \scriptstyle\overset{B\flat{-}37}{\underset{0,4563}{\mathsf{{:}TQ2d}}} &\scriptstyle\overset{B\flat{+}12}{\underset{0,4693}{\mathsf{{:}4Tmt}}} &\scriptstyle\overset{A\sharp{-}48}{\underset{0,4533}{\mathsf{{:}Pn}}} &\scriptstyle\overset{B\flat{-}6}{\underset{0,4644}{\mathsf{{:}Ud2t}}} &.. \\ \scriptstyle\overset{A\natural{-}65}{\underset{0,4237}{\mathsf{{:}R2d}}} &\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}DMmt}}} &\scriptstyle\overset{A\natural{-}53}{\underset{0,4267}{\mathsf{{:}4Tn}}} &\scriptstyle\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}T2Dd2t}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{A\flat{-}19}{\underset{0,4107}{\mathsf{{:}TQmt}}} &\scriptstyle\overset{G\sharp{-}65}{\underset{0,4000}{\mathsf{{:}DMn}}} &\scriptstyle\overset{G\sharp{+}1}{\underset{0,4156}{\mathsf{{:}Pd2t}}} &.. \\ \scriptstyle\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}2TD2d}}} &\scriptstyle\overset{G\natural{-}48}{\underset{0,3813}{\mathsf{{:}Rmt}}} &\scriptstyle\overset{G\natural{-}84}{\underset{0,3733}{\mathsf{{:}TQn}}} &\scriptstyle\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}4Td2t}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{F\sharp{-}113}{\underset{0,3467}{\mathsf{{:}Rn}}} &\scriptstyle\overset{F\sharp{-}16}{\underset{0,3667}{\mathsf{{:}DMd2t}}} &.. \\ \scriptstyle\overset{F\natural{+}45}{\underset{0,3585}{\mathsf{{:}N2d}}} &\scriptstyle\overset{F\natural{+}14}{\underset{0,3520}{\mathsf{{:}2TDmt}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{F\natural{-}35}{\underset{0,3422}{\mathsf{{:}TQd2t}}} &.. \\ \scriptstyle\overset{E\natural{-}20}{\underset{0,3259}{\mathsf{{:}TM2d}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{E\natural{-}51}{\underset{0,3200}{\mathsf{{:}2TDn}}} &\scriptstyle\overset{E\natural{-}63}{\underset{0,3178}{\mathsf{{:}Rd2t}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{E\flat{+}63}{\underset{0,3227}{\mathsf{{:}Nmt}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &.. \\ \scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}2D2d}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}TMmt}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Nn}}} &\scriptstyle\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}2TDd2t}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{C\sharp{-}67}{\underset{0,2667}{\mathsf{{:}TMn}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &.. \\ \scriptstyle\overset{C\natural{-}6}{\underset{0,2607}{\mathsf{{:}3T2d}}} &\scriptstyle\overset{C\natural{+}16}{\underset{0,2640}{\mathsf{{:}2Dmt}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{C\natural{+}47}{\underset{0,2689}{\mathsf{{:}Nd2t}}} &.. \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{B\natural{-}49}{\underset{0,2400}{\mathsf{{:}2Dn}}} &\scriptstyle\overset{B\natural{-}18}{\underset{0,2444}{\mathsf{{:}TMd2t}}} &.. \\ \scriptstyle\overset{B\flat{-}37}{\underset{0,2281}{\mathsf{{:}Q2d}}} &\scriptstyle\overset{B\flat{+}12}{\underset{0,2347}{\mathsf{{:}3Tmt}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &.. \\ \color[rgb]{.6,.6,.6}\square &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{A\natural{-}53}{\underset{0,2133}{\mathsf{{:}3Tn}}} &\scriptstyle\overset{A\natural{\pm}0}{\underset{0,2200}{\mathsf{{:}2Dd2t}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\scriptstyle\overset{A\flat{-}19}{\underset{0,2053}{\mathsf{{:}Qmt}}} &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &.. \\ \scriptstyle\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}TD2d}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{G\natural{-}84}{\underset{0,1867}{\mathsf{{:}Qn}}} &\scriptstyle\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}3Td2t}}} &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &.. \\ \color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{F\natural{+}14}{\underset{0,1760}{\mathsf{{:}TDmt}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{F\natural{-}35}{\underset{0,1711}{\mathsf{{:}Qd2t}}} &.. \\ \scriptstyle\overset{E\natural{-}20}{\underset{0,1630}{\mathsf{{:}M2d}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{E\natural{-}51}{\underset{0,1600}{\mathsf{{:}TDn}}} &\color[rgb]{.6,.6,.6}\square &.. \\ \color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &\color[rgb]{.6,.6,.6}\scriptstyle\blacksquare &.. \\ \color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}Mmt}}} &\color[rgb]{.6,.6,.6}\square &\scriptstyle\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}TDd2t}}} &.. \\ : &: &: &: &\cdot. \end{matrix}\right\} $

[commator]

commator в сообщении #1161867 писал(а):

$ {:}\mathrm{S_{m}}[m/n]s_n\equiv\mathbf{\mbox{[]}}_{i=1}^{k}{\beta_i}\mathrm{S}_{p_i}[\prod_{i=1}^{k}p_i^{\beta_i}/\prod_{i=1}^{k}p_i^{\alpha_i}]\mathbf{\mbox{[]}}_{i=1}^{k}{\alpha_i}\mathrm{s}_{p_i} $

Для $k=11$ и множества соответствий:

$\left\{\left\{ \begin{smallmatrix} \mathrm{\O}\\ \uparrow\\ p_0{=}1\\ \downarrow\\ \mathrm{\o} \end{smallmatrix} \right\}\right. \left. \begin{smallmatrix} {\beta_1}\mathrm{T} &{\beta_2}\mathrm{D} &{\beta_3}\mathrm{M} &{\beta_4}\mathrm{Q} &{\beta_5}\mathrm{N} &{\beta_6}\mathrm{R} &{\beta_7}\mathrm{P} &{\beta_8}\mathrm{U} &{\beta_9}\mathrm{V} &{\beta_{10}}\mathrm{W} &{\beta_{11}}\mathrm{Z} &\cdots \\ \uparrow &\uparrow &\uparrow &\uparrow &\uparrow &\uparrow &\uparrow &\uparrow &\uparrow &\uparrow &\uparrow &\uparrow \\ p_1{=}2 &p_2{=}3 &p_3{=}5 &p_4{=}7 &p_5{=}11 &p_6{=}13 &p_7{=}17 &p_8{=}19 &p_9{=}23 &p_{10}{=}29 &p_{11}{=}31 &\cdots \\ \downarrow &\downarrow &\downarrow &\downarrow &\downarrow &\downarrow &\downarrow &\downarrow &\downarrow &\downarrow &\downarrow &\downarrow \\ {\alpha_1}\mathrm{t} &{\alpha_2}\mathrm{d} &{\alpha_3}\mathrm{m} &{\alpha_4}\mathrm{q} &{\alpha_5}\mathrm{n} &{\alpha_6}\mathrm{r} &{\alpha_7}\mathrm{p} &{\alpha_8}\mathrm{u} &{\alpha_9}\mathrm{v} &{\alpha_{10}}\mathrm{w} &{\alpha_{11}}\mathrm{z} &\cdots \end{smallmatrix} \right\} $,

начальный фрагмент множества всех сочетаний $\mbox{:S}_m\mbox{s}_n$ в системе $\mbox{ЧИП31}{\vee}\mbox{JIL31}$ (чёрные сонанты почти чётко интонированы в системе $\mbox{24РДО}{\vee}\mbox{24EDO}$):

$ \left\{\color[rgb]{.6,.6,.6}\begin{smallmatrix} :&:&:&:&:&:&:&:&:&:&:&:&:&:&.\cdot \\ \blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\overset{D\sharp{+}17}{\underset{0,6286}{\mathsf{{:}DMq}}} &\color[rgb]{.0,.0,.0}\overset{D\sharp{+}3}{\underset{0,6233}{\mathsf{{:}P3t}}} &\overset{E\flat{-}8}{\underset{0,6193}{\mathsf{{:}U2d}}} &\overset{E\flat{-}17}{\underset{0,6160}{\mathsf{{:}DQmt}}} &\overset{D\sharp{-}25}{\underset{0,6133}{\mathsf{{:}Vn}}} &\overset{D\sharp{-}31}{\underset{0,6111}{\mathsf{{:}2Md2t}}} &\overset{E\flat{+}26}{\underset{0,6318}{\mathsf{{:}2TQr}}} \overset{E\flat{+}87}{\underset{0,6544}{\mathsf{{:}Wr}}} &\overset{D\sharp{+}17}{\underset{0,6286}{\mathsf{{:}S_{30}qt}}} \overset{E\flat{+}74}{\underset{0,6495}{\mathsf{{:}Zqt}}} &.. \\ \color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}T\o}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}2Tt}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TDd}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}3T2t}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TMm}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}2TDdt}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TQq}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}4T3t}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}T2D2d}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}S_{20}mt}}} & \overset{D{-}82}{\underset{0,5600}{\mathsf{{:}DQn}}} \color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TNn}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}3TDd2t}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}TRr}}} \color[rgb]{.6,.6,.6}\overset{D{+}63}{\underset{0,6092}{\mathsf{{:}3Dr}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,5867}{\mathsf{{:}2TQqt}}} \color[rgb]{.6,.6,.6}\overset{D{+}59}{\underset{0,6076}{\mathsf{{:}Wqt}}} &.. \\ \blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\overset{C\sharp{-}30}{\underset{0,5448}{\mathsf{{:}Rq}}} &\overset{C\sharp{-}14}{\underset{0,5500}{\mathsf{{:}DM3t}}} &\color[rgb]{.0,.0,.0}\overset{C\sharp{-}1}{\underset{0,5541}{\mathsf{{:}P2d}}} &\overset{D\flat{+}9}{\underset{0,5573}{\mathsf{{:}Umt}}} &\overset{C\sharp{-}67}{\underset{0,5333}{\mathsf{{:}2TMn}}} &\overset{C\sharp{+}24}{\underset{0,5622}{\mathsf{{:}Vd2t}}} &\overset{C\sharp{+}30}{\underset{0,5641}{\mathsf{{:}2Mr}}} &\overset{C\sharp{-}30}{\underset{0,5448}{\mathsf{{:}TRqt}}} \overset{C\sharp{+}35}{\underset{0,5657}{\mathsf{{:}3Dqt}}} &.. \\ \overset{C\natural{\pm}0}{\underset{0,5233}{\mathsf{\square}}} &\square &\square &\overset{C\natural{-}33}{\underset{0,5133}{\mathsf{{:}Q2t}}} &\overset{C\natural{+}16}{\underset{0,5280}{\mathsf{{:}2Dm}}} &\color[rgb]{.0,.0,.0}\overset{C\natural{+}47}{\underset{0,5378}{\mathsf{{:}Ndt}}} &\square &\overset{C\natural{-}33}{\underset{0,5133}{\mathsf{{:}TQ3t}}} &\color[rgb]{.0,.0,.0}\overset{C\natural{-}6}{\underset{0,5215}{\mathsf{{:}4T2d}}} &\overset{C\natural{+}16}{\underset{0,5280}{\mathsf{{:}T2Dmt}}} &\color[rgb]{.0,.0,.0}\overset{C\natural{-}56}{\underset{0,5067}{\mathsf{{:}Un}}} & \overset{C\natural{-}33}{\underset{0,5133}{\mathsf{{:}DQd2t}}} \color[rgb]{.0,.0,.0}\overset{C\natural{+}47}{\underset{0,5378}{\mathsf{{:}TNd2t}}} &\overset{C\natural{+}59}{\underset{0,5415}{\mathsf{{:}3TDr}}} &\color[rgb]{.0,.0,.0}\overset{B\sharp{+}2}{\underset{0,5238}{\mathsf{{:}2Mqt}}} &.. \\ \overset{B\natural{\pm}0}{\underset{0,4939}{\mathsf{\square}}} &\square &\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}Md}}} &\square &\square &\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}TMdt}}} &\overset{B\natural{+}31}{\underset{0,5029}{\mathsf{{:}2TDq}}} &\overset{B\natural{-}61}{\underset{0,4767}{\mathsf{{:}R3t}}} &\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}DM2d}}} &\overset{B\natural{+}17}{\underset{0,4987}{\mathsf{{:}Pmt}}} &\color[rgb]{.0,.0,.0}\overset{B\natural{-}49}{\underset{0,4800}{\mathsf{{:}T2Dn}}} &\overset{B\natural{-}18}{\underset{0,4889}{\mathsf{{:}2TMd2t}}} &\overset{B\natural{+}86}{\underset{0,5190}{\mathsf{{:}Vr}}} &\overset{B\natural{+}31}{\underset{0,5029}{\mathsf{{:}3TDqt}}} &.. \\ \blacksquare &\blacksquare &\blacksquare &\blacksquare &\overset{B\flat{+}12}{\underset{0,4693}{\mathsf{{:}3Tm}}} &\blacksquare &\blacksquare &\blacksquare &\overset{B\flat{-}37}{\underset{0,4563}{\mathsf{{:}TQ2d}}} &\overset{B\flat{+}12}{\underset{0,4693}{\mathsf{{:}4Tmt}}} &\color[rgb]{.0,.0,.0}\overset{A\sharp{-}48}{\underset{0,4533}{\mathsf{{:}Pn}}} &\color[rgb]{.0,.0,.0}\overset{B\flat{-}6}{\underset{0,4644}{\mathsf{{:}Ud2t}}} &\overset{B\flat{+}28}{\underset{0,4738}{\mathsf{{:}DQr}}} \overset{B\flat{+}109}{\underset{0,4964}{\mathsf{{:}TNr}}} &\overset{A\sharp{+}57}{\underset{0,4819}{\mathsf{{:}Vqt}}} &.. \\ \overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{\square}}} &\color[rgb]{.0,.0,.0}\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}Dt}}} &\square &\color[rgb]{.0,.0,.0}\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}TD2t}}} &\square &\color[rgb]{.0,.0,.0}\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}2Ddt}}} &\overset{A\natural{+}81}{\underset{0,4610}{\mathsf{{:}Nq}}} &\color[rgb]{.0,.0,.0}\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}S_{12}3t}}} &\overset{A\natural{-}65}{\underset{0,4237}{\mathsf{{:}R2d}}} &\color[rgb]{.0,.0,.0}\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}DMmt}}} &\color[rgb]{.0,.0,.0}\overset{A\natural{-}53}{\underset{0,4267}{\mathsf{{:}4Tn}}} &\color[rgb]{.0,.0,.0}\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}T2Dd2t}}} &\color[rgb]{.0,.0,.0}\overset{A\natural{+}44}{\underset{0,4513}{\mathsf{{:}2TMr}}} &\color[rgb]{.0,.0,.0}\overset{A\natural{\pm}0}{\underset{0,4400}{\mathsf{{:}DQqt}}} \color[rgb]{.6,.6,.6}\overset{A\natural{+}81}{\underset{0,4610}{\mathsf{{:}TNqt}}} &.. \\ \blacksquare &\blacksquare &\blacksquare &\blacksquare &\overset{A\flat{-}19}{\underset{0,4107}{\mathsf{{:}Qm}}} &\blacksquare &\overset{G\sharp{+}16}{\underset{0,4190}{\mathsf{{:}TMq}}} &\blacksquare &\blacksquare &\overset{A\flat{-}19}{\underset{0,4107}{\mathsf{{:}TQmt}}} &\overset{G\sharp{-}65}{\underset{0,4000}{\mathsf{{:}DMn}}} &\color[rgb]{.0,.0,.0}\overset{G\sharp{+}1}{\underset{0,4156}{\mathsf{{:}Pd2t}}} &\color[rgb]{.0,.0,.0}\overset{A\flat{+}55}{\underset{0,4287}{\mathsf{{:}Ur}}} &\overset{G\sharp{+}16}{\underset{0,4190}{\mathsf{{:}2TMqt}}} &.. \\ \overset{G\natural{\pm}0}{\underset{0,3920}{\mathsf{\square}}} &\square &\color[rgb]{.0,.0,.0}\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}2Td}}} &\square &\square &\color[rgb]{.0,.0,.0}\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}3Tdt}}} &\square &\color[rgb]{.0,.0,.0}\overset{G\natural{+}49}{\underset{0,4033}{\mathsf{{:}N3t}}} &\color[rgb]{.0,.0,.0}\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}2TD2d}}} &\color[rgb]{.0,.0,.0}\overset{G\natural{-}48}{\underset{0,3813}{\mathsf{{:}Rmt}}} &\overset{G\natural{-}84}{\underset{0,3733}{\mathsf{{:}TQn}}} &\color[rgb]{.0,.0,.0}\overset{G\natural{-}4}{\underset{0,3911}{\mathsf{{:}4Td2t}}} &\overset{G\natural{+}61}{\underset{0,4062}{\mathsf{{:}T2Dr}}} &\overset{G\natural{+}27}{\underset{0,3981}{\mathsf{{:}Uqt}}} &.. \\ \blacksquare &\blacksquare &\blacksquare &\overset{F\sharp{-}16}{\underset{0,3667}{\mathsf{{:}M2t}}} &\blacksquare &\blacksquare &\overset{F\sharp{+}33}{\underset{0,3771}{\mathsf{{:}2Dq}}} &\overset{F\sharp{-}16}{\underset{0,3667}{\mathsf{{:}TM3t}}} &\blacksquare &\blacksquare &\overset{F\sharp{-}113}{\underset{0,3467}{\mathsf{{:}Rn}}} &\overset{F\sharp{-}16}{\underset{0,3667}{\mathsf{{:}DMd2t}}} &\overset{F\sharp{+}62}{\underset{0,3836}{\mathsf{{:}Pr}}} &\overset{F\sharp{+}33}{\underset{0,3771}{\mathsf{{:}T2Dqt}}} &.. \\ \overset{F\natural{\pm}0}{\underset{0,3492}{\mathsf{\square}}} &\square &\square &\square &\overset{F\natural{+}14}{\underset{0,3520}{\mathsf{{:}TDm}}} &\overset{F\natural{-}35}{\underset{0,3422}{\mathsf{{:}Qdt}}} &\square &\square &\color[rgb]{.0,.0,.0}\overset{F\natural{+}45}{\underset{0,3585}{\mathsf{{:}N2d}}} &\overset{F\natural{+}14}{\underset{0,3520}{\mathsf{{:}2TDmt}}} &\square &\overset{F\natural{-}35}{\underset{0,3422}{\mathsf{{:}TQd2t}}} &\overset{F\natural{+}58}{\underset{0,3610}{\mathsf{{:}4Tr}}} &\overset{E\sharp{+}34}{\underset{0,3562}{\mathsf{{:}Pqt}}} &.. \\ \overset{E\natural{\pm}0}{\underset{0,3296}{\mathsf{\square}}} &\square &\square &\square &\square &\square &\overset{E\natural{+}29}{\underset{0,3352}{\mathsf{{:}3Tq}}} &\color[rgb]{.0,.0,.0}\overset{E\natural{+}2}{\underset{0,3300}{\mathsf{{:}2D3t}}} &\overset{E\natural{-}20}{\underset{0,3259}{\mathsf{{:}TM2d}}} &\square &\color[rgb]{.0,.0,.0}\overset{E\natural{-}51}{\underset{0,3200}{\mathsf{{:}2TDn}}} &\overset{E\natural{-}63}{\underset{0,3178}{\mathsf{{:}Rd2t}}} &\color[rgb]{.0,.0,.0}\overset{E\natural{+}46}{\underset{0,3385}{\mathsf{{:}DMr}}} &\overset{E\natural{+}29}{\underset{0,3352}{\mathsf{{:}4Tqt}}} &.. \\ \blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\overset{E\flat{+}63}{\underset{0,3227}{\mathsf{{:}Nmt}}} &\blacksquare &\blacksquare &\overset{E\flat{+}26}{\underset{0,3159}{\mathsf{{:}TQr}}} &\overset{D\sharp{+}17}{\underset{0,3143}{\mathsf{{:}DMqt}}} &.. \\ \color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}\O\o}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Tt}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Dd}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}2T2t}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Mm}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}TDdt}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Qq}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}3T3t}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}2D2d}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}TMmt}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Nn}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}2TDd2t}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}Rr}}} &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,2933}{\mathsf{{:}TQqt}}} &.. \\ \blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\overset{C\sharp{-}67}{\underset{0,2667}{\mathsf{{:}TMn}}} &\blacksquare &\blacksquare &\overset{C\sharp{-}30}{\underset{0,2724}{\mathsf{{:}Rqt}}} &.. \\ \overset{C\natural{\pm}0}{\underset{0,2616}{\mathsf{\square}}} &\square &\square &\square &\square &\square &\square &\overset{C\natural{-}33}{\underset{0,2567}{\mathsf{{:}Q3t}}} &\color[rgb]{.0,.0,.0}\overset{C\natural{-}6}{\underset{0,2607}{\mathsf{{:}3T2d}}} &\overset{C\natural{+}16}{\underset{0,2640}{\mathsf{{:}2Dmt}}} &\square &\color[rgb]{.0,.0,.0}\overset{C\natural{+}47}{\underset{0,2689}{\mathsf{{:}Nd2t}}} &\overset{C\natural{+}59}{\underset{0,2708}{\mathsf{{:}2TDr}}} &\square &.. \\ \overset{B\natural{\pm}0}{\underset{0,2469}{\mathsf{\square}}} &\square &\square &\square &\square &\overset{B\natural{-}18}{\underset{0,2444}{\mathsf{{:}Mdt}}} &\overset{B\natural{+}31}{\underset{0,2514}{\mathsf{{:}TDq}}} &\square &\square &\square &\color[rgb]{.0,.0,.0}\overset{B\natural{-}49}{\underset{0,2400}{\mathsf{{:}2Dn}}} &\overset{B\natural{-}18}{\underset{0,2444}{\mathsf{{:}TMd2t}}} &\square &\overset{B\natural{+}31}{\underset{0,2514}{\mathsf{{:}2TDqt}}} &.. \\ \blacksquare &\blacksquare &\blacksquare &\blacksquare &\overset{B\flat{+}12}{\underset{0,2347}{b\mathsf{{:}2Tm}}} &\blacksquare &\blacksquare &\blacksquare &\overset{B\flat{-}37}{\underset{0,2281}{\mathsf{{:}Q2d}}} &\overset{B\flat{+}12}{\underset{0,2347}{\mathsf{{:}3Tmt}}} &\blacksquare &\blacksquare &\overset{B\flat{+}109}{\underset{0,2482}{\mathsf{{:}Nr}}} &\blacksquare &.. \\ \overset{A\natural{\pm}0}{\underset{0,2200}{\mathsf{\square}}} &\square &\square &\color[rgb]{.0,.0,.0}\overset{A\natural{\pm}0}{\underset{0,2200}{\mathsf{{:}D2t}}} &\square &\square &\square &\color[rgb]{.0,.0,.0}\overset{A\natural{\pm}0}{\underset{0,2200}{\mathsf{{:}TD3t}}} &\square &\square &\color[rgb]{.0,.0,.0}\overset{A\natural{-}53}{\underset{0,2133}{\mathsf{{:}3Tn}}} &\color[rgb]{.0,.0,.0}\overset{A\natural{\pm}0}{\underset{0,2200}{\mathsf{{:}2Dd2t}}} &\color[rgb]{.0,.0,.0}\overset{A\natural{+}44}{\underset{0,2256}{\mathsf{{:}TMr}}} &\overset{A\natural{+}81}{\underset{0,2305}{\mathsf{{:}Nqt}}} &.. \\ \blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\overset{G\sharp{+}16}{\underset{0,2095}{\mathsf{{:}Mq}}} &\blacksquare &\blacksquare &\overset{A\flat{-}19}{\underset{0,2053}{\mathsf{{:}Qmt}}} &\blacksquare &\blacksquare &\blacksquare &\overset{G\sharp{+}16}{\underset{0,2095}{\mathsf{{:}TMqt}}} &.. \\ \overset{G\natural{\pm}0}{\underset{0,1960}{\mathsf{\square}}} &\square &\color[rgb]{.0,.0,.0}\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}Td}}} &\square &\square &\color[rgb]{.0,.0,.0}\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}2Tdt}}} &\square &\square &\color[rgb]{.0,.0,.0}\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}TD2d}}} &\square &\overset{G\natural{-}84}{\underset{0,1867}{\mathsf{{:}Qn}}} &\color[rgb]{.0,.0,.0}\overset{G\natural{-}4}{\underset{0,1956}{\mathsf{{:}3Td2t}}} &\overset{G\natural{+}61}{\underset{0,2031}{\mathsf{{:}2Dr}}} &\square &.. \\ \blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\overset{F\sharp{-}16}{\underset{0,1833}{\mathsf{{:}M3t}}} &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\overset{F\sharp{+}33}{\underset{0,1886}{\mathsf{{:}2Dqt}}} &.. \\ \overset{F\natural{\pm}0}{\underset{0,1746}{\mathsf{\square}}} &\square &\square &\square &\overset{F\natural{+}14}{\underset{0,1760}{\mathsf{{:}Dm}}} &\square &\square &\square &\square &\overset{F\natural{+}14}{\underset{0,1760}{\mathsf{{:}TDmt}}} &\square &\overset{F\natural{-}35}{\underset{0,1711}{\mathsf{{:}Qd2t}}} &\overset{F\natural{+}58}{\underset{0,1805}{\mathsf{{:}3Tr}}} &\square &.. \\ \overset{E\natural{\pm}0}{\underset{0,1648}{\mathsf{\square}}} &\square &\square &\square &\square &\square &\overset{E\natural{+}29}{\underset{0,1676}{\mathsf{{:}2Tq}}} &\square &\overset{E\natural{-}20}{\underset{0,1630}{\mathsf{{:}M2d}}} &\square &\color[rgb]{.0,.0,.0}\overset{E\natural{-}51}{\underset{0,1600}{\mathsf{{:}TDn}}} &\square &\square &\overset{E\natural{+}29}{\underset{0,1676}{\mathsf{{:}3Tqt}}} &.. \\ \blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\overset{E\flat{+}26}{\underset{0,1579}{\mathsf{{:}Qr}}} &\blacksquare &.. \\ \overset{D\natural{\pm}0}{\underset{0,1468}{\mathsf{\square}}} &\square &\square &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}T2t}}} &\square &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}Ddt}}} &\square &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}2T3t}}} &\square &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}Mmt}}} &\square &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}TDd2t}}} &\square &\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{0,1467}{\mathsf{{:}Qqt}}} &.. \\ \blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\blacksquare &\overset{C\sharp{-}67}{{\mathsf{{:}Mn}}} &\blacksquare &\blacksquare &\blacksquare &.. \\ :&:&:&:&:&:&:&:&:&:&:&:&:&:&\cdot. \end{smallmatrix}\color[rgb]{.0,.0,.0}\right\} $

[commator]

Свободный Художник в сообщении #1091322 писал(а):

Определение унарных операций $VR$ и $HR$:
$VR\left(\dfrac{m}{n}\right) = \dfrac{m}{1},
$HR\left(\dfrac{m}{n}\right) = \dfrac{1}{n}$.

$VR\left(\dfrac{0}{0}\right) = \dfrac{0}{1}, HR\left(\dfrac{0}{0}\right) = \dfrac{1}{0}$.

Такое допустимо?

[commator]

Математик в Сети писал(а):

Операции V и H могут по разному представляться

Мне раньше казалось, что Ваши V и H не очень удачные обозначения, но теперь понимаю: даже очень удачные из-за

Свободный Художник в сообщении #1091322 писал(а):

унарных операций $VR$ и $HR$:
$VR\left(\dfrac{m}{n}\right) = \dfrac{m}{1},
$HR\left(\dfrac{m}{n}\right) = \dfrac{1}{n}$.

Потому что для со́звуков естественным проявлением оберсвойств нахожу музыкальную вертикаль, а унтерсвойств ― музыкальную горизонталь.

commator в сообщении #1092124 писал(а):

В музыке по горизонтали измеряется время, по вертикали ― высота

[Свободный Художник]

Мне представляется, что $V$ и $H$ являются удачными конструкциями, потому что они улавливают нечто фундаментальное в арифметике периода ее инициации:

Свободный Художник в сообщении #1160677 писал(а):

Свободный Художник в сообщении #1159741 писал(а):

Обратите внимание также и на то, что некоторые провозглашают существование в античности некоей "независимой науки гармоники":
http://www.px-pict.com/7/3/2/1/12/0/3.html
(ссылка из книги Е. Герцмана)

Свободный Художник в сообщении #1160375 писал(а):

Возможно, что это было одной из ранних разновидностей "теории всего":
http://www.px-pict.com/9/6/6/10/1/2.html
Зародившись из задач теории музыки, она пыталась затем примениться и к другим предметным областям.

Как следует из исследований Б. Л. ван дер Вардена:
http://www.px-pict.com/7/3/1/8/0.html
математическое ядро этой "Гармоники" составляли 7-я и 8-я книги "Начал" Евклида, а также сочинение "Sectio Canonis":
http://www.nsu.ru/classics/pythagoras/S ... anonis.pdf

По этой причине я позволил себе назвать операторы $V$ и $H$ ян- и инь- конструкторами музыкальных интервалов:
http://www.px-pict.com/9/6/8/2/1/1.html

-- Чт ноя 17, 2016 13:33:26 --

Томас Манн в своем мифологическом романе в качестве одного из примеров того, что имеет обыкновение воссоздаваться снова и снова, привел Великую Башню:
http://www.px-pict.com/11/1/1/5.html

Думается, что и Великое Дерево:
http://www.px-pict.com/10/4/4/13.html
которое мы уже много обсуждали, тоже обладает таким свойством. В пользу этого предположения говорит, например, возникновение на определенном этапе теории сюрреальных чисел:
http://kvant.mccme.ru/1979/11/syurrealnye_chisla.htm

Получается, что по какой-то причине Великое Дерево является весьма любезным нашему мышлению.

[commator]

Свободный Художник в сообщении #1169654 писал(а):

Великое Дерево

Распятие в клавишно-временных состояниях системы $\mbox{12РДО}{\vee}\mathrm{12EDO}$:

$\left\{\begin{matrix} \color[rgb]{.6,.6,.6}\xymatrix @W=0pc @H=0pc @C=.4pc @R=0pc {% :&:&:&:&:&:&:&:&:&:&:&:&:&:&.\cdot \\ \color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{D\natural{-}2}{\underset{}{\mathsf{{:}T[2/1]\o}}} \ar '[5,1]'[7,2]'[8,3]'[9,4]'[9,5]'[10,6]'[10,7]'[10,8]'[11,9]'[10,10]'[10,11]'[11,12]'[11,13]'[11,14]+R &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &.. \\ \bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\scriptscriptstyle\overset{C\sharp{-}30}{\underset{}{\mathsf{{:}R[13/7]q}}} &\scriptscriptstyle\overset{C\sharp{-}14}{\underset{}{\mathsf{{:}DM[15/8]3t}}} &\color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{C\sharp{-}1}{\underset{}{\mathsf{{:}P[17/9]2d}}} &\bullet &\bullet &\bullet &\bullet &\bullet &.. \\ \circ &\circ &\circ &\scriptscriptstyle\overset{C\natural{-}33}{\underset{}{\mathsf{{:}Q[7/4]2t}}} \ar '[1,3]'[1,4]+UR'[1,6] &\scriptscriptstyle\overset{C\natural{+}16}{\underset{}{\mathsf{{:}2D[9/5]m}}} \ar '[,1]+DR'[,4]'[,8] &\color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{C\natural{+}47}{\underset{}{\mathsf{{:}N[11/6]dt}}} \ar '[-1,5]'[-1,9]+R &\circ &\circ &\color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{C\natural{-}6}{\underset{}{\mathsf{{:}4T[16/9]2d}}} &\circ &\circ &\circ &\circ &\circ &.. \\ \circ &\circ &\scriptscriptstyle\overset{B\natural{-}18}{\underset{}{\mathsf{{:}M[5/3]d}}} \ar '[1,2]'[2,4]'[1,6]'[2,8] &\circ &\circ &\circ &\scriptscriptstyle\overset{B\natural{+}31}{\underset{}{\mathsf{{:}2TD[12/7]q}}} &\scriptscriptstyle\overset{B\natural{-}61}{\underset{}{\mathsf{{:}R[13/8]3t}}} &\circ &\circ &\circ &\circ &\circ &\circ &.. \\ \bullet &\bullet &\bullet &\bullet &\scriptscriptstyle\overset{B\flat{+}12}{\underset{}{\mathsf{{:}3T[8/5]m}}} \ar '[-1,3]'[-1,6] &\bullet &\bullet &\bullet &\scriptscriptstyle\overset{B\flat{-}37}{\underset{}{\mathsf{{:}TQ[14/9]2d}}} &\bullet &\bullet &\bullet &\bullet &\bullet &.. \\ \circ &\color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{A\natural{\pm}0}{\underset{}{\mathsf{{:}D[3/2]t}}} \ar '[-2,1]'[-3,2]'[-3,3]'[-3,4]'[-4,5]'[-4,6]'[-4,7]'[-4,8]'[-5,9]'[-4,10]'[-4,11]'[-5,12]'[-5,13]+R &\circ &\circ &\circ &\circ &\scriptscriptstyle\overset{A\natural{+}81}{\underset{}{\mathsf{{:}N[11/7]q}}} &\circ &\scriptscriptstyle\overset{A\natural{-}65}{\underset{}{\mathsf{{:}R2[13/9]d}}} &\circ &\circ &\circ &\circ &\circ &.. \\ \bullet &\bullet &\bullet &\bullet &\scriptscriptstyle\overset{A\flat{-}19}{\underset{}{\mathsf{{:}Q[7/5]m}}} \ar '[1,3]'[1,6] &\bullet &\scriptscriptstyle\overset{G\sharp{+}16}{\underset{}{\mathsf{{:}TM[10/7]q}}} &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &.. \\ \circ &\circ &\color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{G\natural{-}4}{\underset{}{\mathsf{{:}2T[4/3]d}}} \ar '[-1,2]'[-1,4]'[-2,6]'[-2,8] &\circ &\circ &\circ &\circ &\color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{G\natural{+}49}{\underset{}{\mathsf{{:}N[11/8]3t}}} &\circ &\circ &\circ &\circ &\circ &\circ &.. \\ \bullet &\bullet &\bullet &\scriptscriptstyle\overset{F\sharp{-}16}{\underset{}{\mathsf{{:}M[5/4]2t}}} \ar '[,3]'[-1,6] &\bullet &\bullet &\scriptscriptstyle\overset{F\sharp{+}33}{\underset{}{\mathsf{{:}2D[9/7]q}}} &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &.. \\ \circ &\circ &\circ &\circ &\scriptscriptstyle\overset{F\natural{+}14}{\underset{}{\mathsf{{:}TD[6/5]m}}} \ar '[,1]+UR'[,4]'[,8] &\scriptscriptstyle\overset{F\natural{-}35}{\underset{}{\mathsf{{:}Q[7/6]dt}}} \ar '[-1,5]'[,9]+R &\circ &\circ &\color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{F\natural{+}45}{\underset{}{\mathsf{{:}N[11/9]2d}}} &\circ &\circ &\circ &\circ &\circ &.. \\ \circ &\circ &\circ &\circ &\circ &\circ &\scriptscriptstyle\overset{E\natural{+}29}{\underset{}{\mathsf{{:}3T[8/7]q}}} &\color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{E\natural{+}2}{\underset{}{\mathsf{{:}2D[9/8]3t}}} &\scriptscriptstyle\overset{E\natural{-}20}{\underset{}{\mathsf{{:}TM[10/9]2d}}} &\circ &\circ &\circ &\circ &\circ &.. \\ \bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &.. \\ \color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{D\natural{-}2}{\underset{}{\mathsf{{:}\O[1/1]\o}}} \ar '[-12,]'[-13,]+U \ar '[12,1]'[13,2]+DL &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &.. \\ \bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &.. \\ \circ &\circ &\circ &\circ &\circ &\circ &\circ &\scriptscriptstyle\overset{C\natural{-}33}{\underset{}{\mathsf{{:}Q[7/8]3t}}} &\color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{C\natural{-}6}{\underset{}{\mathsf{{:}3T[8/9]2d}}} &\circ &\circ &\circ &\circ &\circ &.. \\ \circ &\circ &\circ &\circ &\circ &\scriptscriptstyle\overset{B\natural{-}18}{\underset{}{\mathsf{{:}M[5/6]dt}}} \ar '[,1]+DR'[,5]'[,9]+R &\scriptscriptstyle\overset{B\natural{+}31}{\underset{}{\mathsf{{:}TD[6/7]q}}} &\circ &\circ &\circ &\circ &\circ &\circ &\circ &.. \\ \bullet &\bullet &\bullet &\bullet &\scriptscriptstyle\overset{B\flat{+}12}{\underset{}{\mathsf{{:}2T[4/5]m}}} \ar '[,4]'[,8] &\bullet &\bullet &\bullet &\scriptscriptstyle\overset{B\flat{-}37}{\underset{}{\mathsf{{:}Q[7/9]2d}}} &\bullet &\bullet &\bullet &\bullet &\bullet &.. \\ \circ &\circ &\circ &\color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{A\natural{\pm}0}{\underset{}{\mathsf{{:}D[3/4]2t}}} \ar '[1,3]'[1,6] &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &.. \\ \bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\scriptscriptstyle\overset{G\sharp{+}16}{\underset{}{\mathsf{{:}M[5/7]q}}} &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &.. \\ \circ &\circ &\color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{G\natural{-}4}{\underset{}{\mathsf{{:}T[2/3]d}}} \ar '[2,2]'[3,4]'[3,6]'[3,8] &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &.. \\ \bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\scriptscriptstyle\overset{F\sharp{-}16}{\underset{}{\mathsf{{:}M[5/8]3t}}} &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &.. \\ \circ &\circ &\circ &\circ &\scriptscriptstyle\overset{F\natural{+}14}{\underset{}{\mathsf{{:}D[3/5]m}}} \ar '[-1,3]'[-1,6] &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &.. \\ \circ &\circ &\circ &\circ &\circ &\circ &\scriptscriptstyle\overset{E\natural{+}29}{\underset{}{e\mathsf{{:}2T[4/7]q}}} &\circ &\scriptscriptstyle\overset{E\natural{-}20}{\underset{}{\mathsf{{:}M[5/9]2d}}} &\circ &\circ &\circ &\circ &\circ &.. \\ \bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &.. \\ \circ &\color[rgb]{.0,.0,.0}\scriptscriptstyle\overset{D\natural{-}2}{\underset{}{\mathsf{{:}\O[1/2]t}}} \ar '[-5,1]'[-7,2]'[-8,3]'[-9,4]'[-9,5]'[-10,6]'[-10,7]'[-10,8]'[-11,9]'[-10,10]'[-10,11]'[-11,12]'[-11,13]+R &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &.. \\ :&:&:&:&:&:&:&:&:&:&:&:&:&:&\cdot. }\color[rgb]{.0,.0,.0} \end{matrix}\right\}$

[commator]

commator в сообщении #1170066 писал(а):

Свободный Художник в сообщении #1169654 писал(а):

Великое Дерево

Распятие в клавишно-временных состояниях системы $\mbox{12РДО}{\vee}\mathrm{12EDO}$:

под воздействием высотных изгибов Оно расправляет ветви, что показывает набросок унтерфрагмента в пределах от $\overset{D\natural{-}2}{\underset{[1/1]}{\mathsf{{:}\O\o}}}$ до $\overset{D\natural{-}2}{\underset{[1/2]}{\mathsf{{:}\O t}}}}$:

$\left\{\begin{matrix} \color[rgb]{.6,.6,.6}\xymatrix @W=0pc @H=0pc @C=12pt @R=18.5pt {% :&:&:&:&:&:&:&:&:&:&:&:&:&:&:&:&.\cdot \\ \circ\ar'[]*{\scriptstyle\circ}_<{\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{[1/1]}{\mathsf{{:}\O\o}}}} '[12,1]'[13,2]+DL &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &.. \\ \bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet\ar'[]-<,6.7mm>*{\scriptstyle\bullet}_<{\overset{C\sharp{-}67}{\underset{[10/11]}{\mathsf{{:}TMn}}}} &\bullet &\bullet &\bullet\ar'[]-<,3mm>*{\scriptstyle\bullet}_<{\overset{C\sharp{-}30}{\underset{[13/14]}{\mathsf{{:}Rqt}}}} &\bullet\ar'[]-<,2.1mm>*{\scriptstyle\bullet}_<{\overset{D\flat{-}21}{\underset{[14/15]}{\mathsf{{:}TQmd}}}} &\bullet\ar'[]-<,1.4mm>*{\scriptstyle\bullet}^<{\overset{C\sharp{-}14}{\underset{[15/16]}{\mathsf{{:}DM4t}}}} &.. \\ \circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ\ar'[]-<,3.3mm>*{\scriptstyle\circ}_<{\overset{C\natural{-}33}{\underset{[7/8]}{\mathsf{{:}Q3t}}}} &\circ\ar'[]*{\scriptstyle\circ}_<{\color[rgb]{.0,.0,.0}\overset{C\natural{-}6}{\underset{[8/9]}{\mathsf{{:}3T2d}}}} &\circ\ar'[]+<,1.6mm>*{\scriptstyle\circ}_<{\overset{C\natural{+}16}{\underset{[9/10]}{\mathsf{{:}2Dmt}}}} &\circ &\circ\ar'[]+<,4.7mm>*{\scriptstyle\circ}^<{\color[rgb]{.0,.0,.0}\overset{C\natural{+}47}{\underset{[11/12]}{\mathsf{{:}Nd2t}}}} &\circ\ar'[]+<,5.9mm>*{\scriptstyle\circ}^<{\overset{C\natural{+}59}{\underset{[12/13]}{\mathsf{{:}2TDr}}}} &\circ &\circ &\circ &.. \\ \circ &\circ &\circ &\circ &\circ &\circ\ar'[]-<,1.8mm>*{\scriptstyle\circ}^<{\overset{B\natural{-}18}{\underset{[5/6]}{\mathsf{{:}Mdt}}}} '[1,11]+<2mm,3mm> &\circ\ar'[]+<,3.1mm>*{\scriptstyle\circ}^<{\overset{B\natural{+}31}{\underset{[6/7]}{\mathsf{{:}TDq}}}} '[,10]+R &\circ &\circ &\circ &\circ\ar'[]-<,4.9mm>*{\scriptstyle\circ}_<{\color[rgb]{.0,.0,.0}\overset{B\natural{-}49}{\underset{[9/11]}{\mathsf{{:}2Dn}}}} '[,6]+<2mm,-3.8mm> &\circ &\circ &\circ &\circ &\circ\ar'[]-<,6.1mm>*{\scriptstyle\circ}_<{\overset{B\natural{-}61}{\underset{[13/16]}{\mathsf{{:}R4t}}}} &.. \\ \bullet &\bullet &\bullet &\bullet &\bullet\ar'[]+<,1.2mm>*{\scriptstyle\bullet}_<{\overset{B\flat{+}12}{\underset{[4/5]}{\mathsf{{:}2Tm}}}} '[,1]+DL'[,12]+<2mm,-7mm> &\bullet &\bullet &\bullet &\bullet\ar'[]-<,3.7mm>*{\scriptstyle\bullet}_<{\overset{B\flat{-}37}{\underset{[7/9]}{\mathsf{{:}Q2d}}}} '[,8]+DR &\bullet &\bullet &\bullet &\bullet\ar'[]+<,10.9mm>*{\scriptstyle\bullet}^<{\overset{B\flat{+}109}{\underset{[11/13]}{\mathsf{{:}Nr}}}} &\bullet &\bullet &\bullet &.. \\ \circ &\circ &\circ &\circ\ar'[]*{\scriptstyle\circ}^<{\color[rgb]{.0,.0,.0}\overset{A\natural{\pm}0}{\underset{[3/4]}{\mathsf{{:}D2t}}}} '[1,4]+DR'[2,13]+<2mm,4mm> &\circ &\circ &\circ &\circ &\circ &\circ &\circ\ar'[]-<,5.3mm>*{\scriptstyle\circ}_<{\color[rgb]{.0,.0,.0}\overset{A\natural{-}53}{\underset{[8/11]}{\mathsf{{:}3Tn}}}} &\circ &\circ\ar'[]+<,4.4mm>*{\scriptstyle\circ}^<{\color[rgb]{.0,.0,.0}\overset{A\natural{+}44}{\underset{[10/13]}{\mathsf{{:}TMr}}}} &\circ\ar'[]+<,8.1mm>*{\scriptstyle\circ}^<{\overset{A\natural{+}81}{\underset{[11/14]}{\mathsf{{:}Nqt}}}} &\circ &\circ &.. \\ \bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet\ar'[]+<,1.6mm>*{\scriptstyle\bullet}_<{\overset{G\sharp{+}16}{\underset{[5/7]}{\mathsf{{:}Mq}}}} '[-1,10]+DR &\bullet &\bullet &\bullet\ar'[]-<,1.9mm>*{\scriptstyle\bullet}_{\overset{A\flat{-}19}{\underset{[7/10]}{\mathsf{{:}Qmt}}}} &\bullet &\bullet &\bullet &\bullet &\bullet\ar'[]+<,6.1mm>*{\scriptstyle\bullet}^{\overset{A\flat{+}61}{\underset{[11/15]}{\mathsf{{:}Nmd}}}} &\bullet &.. \\ \circ &\circ &\circ\ar'[]*{\scriptstyle\circ}^<{\color[rgb]{.0,.0,.0}\overset{G\natural{-}4}{\underset{[2/3]}{\mathsf{{:}Td}}}} '[2,2]+U'[3,4]+UR'[3,6]+DL'[4,14]+RD &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ\ar'[]-<,8.4mm>*{\scriptstyle\circ}_<{\overset{G\natural{-}84}{\underset{[7/11]}{\mathsf{{:}Qn}}}} &\circ &\circ\ar'[]+<,6.1mm>*{\scriptstyle\circ}^<{\overset{G\natural{+}61}{\underset{[9/13]}{\mathsf{{:}2Dr}}}} &\circ &\circ &\circ\ar'[]+<,4.9mm>*{\scriptstyle\circ}^<{\color[rgb]{.0,.0,.0}\overset{G\natural{+}49}{\underset{[11/16]}{\mathsf{{:}N4t}}}} &.. \\ \bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet\ar'[]-<,1.6mm>*{\scriptstyle\bullet}^<{\overset{F\sharp{-}16}{\underset{[5/8]}{\mathsf{{:}M3t}}}} '[1,9]+UR &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet\ar'[]+<,3.3mm>*{\scriptstyle\bullet}^<{\overset{F\sharp{+}33}{\underset{[9/14]}{\mathsf{{:}2Dqt}}}} &\bullet &\bullet &.. \\ \circ &\circ &\circ &\circ &\circ\ar'[]+<,1.4mm>*{\scriptstyle\circ}_<{\overset{F\natural{+}14}{\underset{[3/5]}{\mathsf{{:}Dm}}}} '[-1,4]+UR'[-1,12]+<2mm,5mm> &\circ &\circ &\circ &\circ &\circ &\circ &\circ\ar'[]-<,3.5mm>*{\scriptstyle\circ}_<{\overset{F\natural{-}35}{\underset{[7/12]}{\mathsf{{:}Qd2t}}}} [1,5]+<2mm,5mm> &\circ\ar'[]+<,5.8mm>*{\scriptstyle\circ}^<{\overset{F\natural{+}58}{\underset{[8/13]}{\mathsf{{:}3Tr}}}} &\circ &\circ &\circ &.. \\ \circ &\circ &\circ &\circ &\circ &\circ &\circ\ar'[]+<,2.9mm>*{\scriptstyle\circ}^<{\overset{E\natural{+}29}{\underset{[4/7]}{e\mathsf{{:}2Tq}}}} '[-1,10]+DR &\circ &\circ\ar'[]-<,2mm>*{\scriptstyle\circ}_<{\overset{E\natural{-}20}{\underset{[5/9]}{\mathsf{{:}M2d}}}} '[,8]+R &\circ &\circ\ar'[]-<,5.1mm>*{\scriptstyle\circ}_<{\color[rgb]{.0,.0,.0}\overset{E\natural{-}51}{\underset{[6/11]}{\mathsf{{:}TDn}}}} &\circ &\circ &\circ &\circ &\circ\ar'[]*{\scriptstyle\circ}_<{\color[rgb]{.0,.0,.0}\overset{E\natural{+}2}{\underset{[9/16]}{\mathsf{{:}2D4t}}}} &.. \\ \bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet &\bullet\ar'[]+<,2.6mm>*{\scriptstyle\bullet}^<{\overset{E\flat{+}26}{\underset{[7/13]}{\mathsf{{:}Qr}}}} &\bullet &\bullet\ar'[]+<,1mm>*{\scriptstyle\bullet}_<{\overset{E\flat{+}10}{\underset{[8/15]}{\mathsf{{:}3Tmd}}}} &\bullet &.. \\ \circ &\circ\ar'[]*{\scriptstyle\circ}^<{\color[rgb]{.0,.0,.0}\overset{D\natural{-}2}{\underset{[1/2]}{\mathsf{{:}\O t}}}} '[-5,1]'[-7,2]'[-8,3]+U'[-9,4]+R'[-10,7]'[-10,10]+<,4.7mm>[-11,15]+R &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &\circ &.. \\ :&:&:&:&:&:&:&:&:&:&:&:&:&:&:&:&\cdot. }\color[rgb]{.0,.0,.0} \end{matrix}\right\}$

[commator]

Теперь не набросок, а почти чертёж

commator в сообщении #1170412 писал(а):

унтерфрагмента в пределах от $\overset{D\natural{-}2}{\underset{[1/1]}{\mathsf{{:}\O\o}}}$ до $\overset{D\natural{-}2}{\underset{[1/2]}{\mathsf{{:}\O t}}}}$:

Дерево его ветками

commator в сообщении #1048937 писал(а):

в области восприятия через логарифмы слипается

Оберфрагмент в пределах от $\overset{D\natural{-}2}{\underset{[1/1]}{\mathsf{{:}\O\o}}}$ до $\overset{D\natural{-}2}{\underset{[4/1]}{\mathsf{{:}2T\o}}}}$:

[Свободный Художник]

Свободный Художник в сообщении #1169654 писал(а):

Мне представляется, что $V$ и $H$ являются удачными конструкциями, потому что они улавливают нечто фундаментальное в арифметике периода ее инициации ...

Поэтому в качестве изначального остова искомой алгебры музыкальной гармонии можно было бы выбрать абсолютно свободную алгебру с двумя унарными операциями и одним образующим:

Свободный Художник в сообщении #146343 писал(а):

Свободный Художник в сообщении #144875 писал(а):

Например, для $\mathbf{Q^+}$ являются справедливыми, очевидно, следующие два утверждения:
(1) Существует элемент, удовлетворяющий условию $\overline{x} = x$;
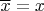
(2) Такой элемент единственен.
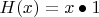
Положив этому элементу естественное имя 1, мы можем определить две двойственные друг по отношению к другу унарные операции: $H(x) = x \bullet 1$ и $V(x) = x \circ 1$.
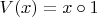
Затем при помощи этих двух унарных операций H и V, примененных в различных комбинациях к 1, мы, как можно показать, можем получить все положительные рациональные числа, причем разным комбинациям будут соответствовать разные числа.
Например, $V(H(H(1))) = 3/4$

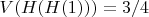
Кстати говоря, система с двумя унарными операциями $V$ и $H$, основанная на системе $\mathbf{Q^+}$, также весьма интересна (обозначим ее $\mathbf{SBT}$):
$\mathbf{SBT} = \langle \, \mathrm{SBT}, V, H, 1 \rangle$,
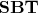
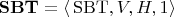
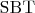
где $\mathrm{SBT}$ есть снова множество положительных рациональных чисел;
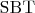
$V$ и $H$ есть унарные операции на множестве $\mathrm{SBT}$, определяемые как указано выше;
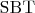
$1$ есть выделенный элемент во множестве $\mathrm{SBT}$.

[Свободный Художник]

Абсолютно свободные алгебры являются объектами "универсальной алгебры". Имея в виду дальнейшее развитие нашего "изначального остова музыкальной гармонии", мы можем сделать еще один небольшой шаг и добавить к абсолютно свободной алгебре немного логики:

Свободный Художник в сообщении #149232 писал(а):

Кажется, в системе $\mathbf{SBT}$ можно очень просто определить отношение $<$ строгого линейного порядка на множестве положительных рациональных чисел. Для этого достаточно постулировать следующие “определяющие соотношения” (которые, очевидно, справедливы при указанной интерпретации операций $V$ и $H$):
(v1). Для любого $x, V(x) < 1$,
(h1). Для любого $x, 1 < H(x)$,
(v2). Если $x < y$, то $V(x) < V(y)$,
(h2). Если $x < y$, то $H(x) < H(y)$,
(trans). Если $x < y$ и $y < z$, то $x < z$.

Докажем, например, что $\dfrac4{7} < \dfrac2{3}$.
$V(H(1)) = \dfrac2{3}$; $V(H(V(V(1)))) = \dfrac4{7}$.

Доказательство.
(1) Для любого $x, V(x) < 1$ -- аксиома (v1);
(2) $V(V(1)) < 1$ -- из (1);
(3) $H(V(V(1))) < H(1)$ -- из (2) по аксиоме (h2);
(4) $V(H(V(V(1)))) < V(H(1))$ -- из (3) по аксиоме (v2).

Поскольку все “определяющие соотношения” являются хорновскими дизъюнктами, то их можно рассматривать как “логическую программу”:
http://www.px-pict.com/9/6/4/4.html,
рекурсивно определяющую на множестве всех основных термов системы $\mathbf{SBT}$ отношение $<$ строгого линейного порядка.

Тогда мы уже, в принципе, попадем под юрисдикцию "теории моделей":
http://www.px-pict.com/9/6/2/8/4/1.html
Причем той ее области, где экспериментальным путем было "нащупано" одно очень удачное сочетание универсальной алгебры и логики. Как это описано в статье-лекции Дж. Робинсона:
http://www.px-pict.com/9/7/4/4/1.html
http://www.px-pict.com/9/7/4/4/1/1.html

Свободный Художник в сообщении #1155397 писал(а):

Все же могут оказаться полезными и другие способы нотации музыкальных сущностей. Зная о Вашей приверженности методам Искусственного Интеллекта, хотел бы обратить Ваше внимание на возможность использования для этой цели "основных термов":
http://www.px-pict.com/9/6/8/2/1/1/2/2/1.html
(пункт 3 на указанной странице)
В духе классической парадигмы "логического программирования":
http://www.px-pict.com/9/6/4/4/1.html
Классическое сочинение в этой области:
Kowalski R. Predicate Logic as Programming Language.
http://www.px-pict.com/9/7/4/4/4.html

[Свободный Художник]

Алгебра "основных термов" -- только одно из возможных представлений нашей абсолютно свободной алгебры:

Свободный Художник в сообщении #1174563 писал(а):

Свободный Художник в сообщении #1169654 писал(а):

Мне представляется, что $V$ и $H$ являются удачными конструкциями, потому что они улавливают нечто фундаментальное в арифметике периода ее инициации ...

Поэтому в качестве изначального остова искомой алгебры музыкальной гармонии можно было бы выбрать абсолютно свободную алгебру с двумя унарными операциями и одним образующим:

Важны также и другие ее представления, например, "геометрическое представление", упомянутое мною здесь:
http://www.px-pict.com/9/6/8/2/1/1/2/2/1.html

С методологической точки зрения во всех этих представлениях нам помогут разобраться ценные рассуждения С. К. Клини о способах введения "систем объектов":
http://www.px-pict.com/9/6/2/8/10/1/2/8.html

Только теперь вместо его системы $S = (D, 0, ')$, которую он использовал в качестве иллюстрации в своих рассуждениях, мы будем рассматривать систему $S = (D, p, V, H)$, где
$D$, как и у Клини, есть некоторое непустое множество ("объектов");
$V, H$ есть некоторые унарные операции, определенные на $D$;
$p$ есть некоторый выделенный элемент множества $D$.

[Свободный Художник]

На том уровне абстракции, который соответствует "алгебре термов":
https://en.wikipedia.org/wiki/Term_algebra
мы в состоянии различать "поверхностное" и "глубинное" деревья:
http://www.px-pict.com/10/4/4/5.html
(пункт 3 на указанной странице)

При этом достаточно использовать только самые основные конструкции универсальной алгебры, как они изложены, например, у Расевой - Сикорского:
http://www.px-pict.com/9/6/2/8/3/1/1/4.html
Предполагается, что $\varphi_{V}$ и $\varphi_{H}$ являются эндоморфизмами нашей алгебры термов, определяемыми равенствами $\varphi_{V}(p) = V(p)$ и $\varphi_{H}(p) = H(p)$, соответственно.
Из того, что $\varphi_{V}$ и $\varphi_{H}$ -- эндоморфизмы, следует, что будут выполняться следующие четыре тождества:
$\forall z [\varphi_{V}(V(z)) = V(\varphi_{V}(z))]$;
$\forall z [\varphi_{V}(H(z)) = H(\varphi_{V}(z))]$;
$\forall z [\varphi_{H}(V(z)) = V(\varphi_{H}(z))]$;
$\forall z [\varphi_{H}(H(z)) = H(\varphi_{H}(z))]$.

[Свободный Художник]

Свободный Художник в сообщении #1155397 писал(а):

Все же могут оказаться полезными и другие способы нотации музыкальных сущностей. Зная о Вашей приверженности методам Искусственного Интеллекта, хотел бы обратить Ваше внимание на возможность использования для этой цели "основных термов":

Здесь нам будут полезны соответствующие конструкции из Computer Science:
"... мы хотим привлечь внимание к вариантам операционного определения, которые позволяют рассматривать равенство или систему равенств как "логическую программу", определяющую "логические вычисления", не похожие на вычисления в традиционных языках программирования или в машинах традиционной архитектуры":
http://www.px-pict.com/9/6/2/2/2.html
В этой связи пояснил в качестве примера действие эндоморфизма $\varphi_{H}$ на терм $V(H(p))$:
http://www.px-pict.com/10/4/4/5.html
(пункт 4 на странице по указанной ссылке)

Свободный Художник в сообщении #1179740 писал(а):

Предполагается, что $\varphi_{V}$ и $\varphi_{H}$ являются эндоморфизмами нашей алгебры термов, определяемыми равенствами $\varphi_{V}(p) = V(p)$ и $\varphi_{H}(p) = H(p)$, соответственно.

[Свободный Художник]

По обсуждаемой здесь проблематике публикации вот этого журнала могут быть полезны:
Journal of Mathematics and Music.
The Journal aims to advance the use of mathematical modelling and computation in music theory. It focuses on mathematical approaches to musical structures and processes, including mathematical investigations into music-theoretic or compositional issues as well as mathematically motivated analyses of musical works or performances. In consideration of the deep unsolved ontological and epistemological questions concerning knowledge about music, the Journal is open to a broad array of methodologies and topics, particularly those outside of established research fields such as acoustics, sound engineering, auditory perception, linguistics etc.
http://www.tandfonline.com/toc/tmam20/current