Непонятно от какого аргумента берётся функция

, предположу что от

, т.к. других буковок в формуле не наблюдается, т.е.

.
Для

значение задано, ок.
Для

значение

, уже не ок, до

нет пар простых близнецов.
Для

значение

тоже не ок, до

всего одна пара простых близнецов:

.
Для

значение

тоже не ок, до

всего две пары простых близнецов:

и

.
Для

значение

ещё более не ок, до

всего
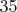
пар простых близнецов.
И?
Вы не так считаете.
Надо так (но надо учесть, что при рассмотрении постоянно "прицепляется" одна пара:

*):
Для

значение

, до

одна пара, взаимно простых с

, но не близнецов-

.*
Для

значение

, до

имеем две пары чисел-близнецов, взаимно-простых с

. Это

и

, а также пара

*
Для

значение

, до

имеем 14 пар чисел-близнецов взаимно простых с

. Это пары простых-близнецов

, а также пара

*, где число

- взаимнопростое.
* Конечно можно и отцепить эту пару, вычитая из

единицу.
-- 15 мар 2021 18:29 --Ну и о чём можно дальше говорить если ложна исходная посылка?!
Я об этом и сказал в сообщении от 14.03 и сегодня.
Указанное выше допущение ведет к погрешности чисел

и

относительно чисел

и

(обозначения из предыдущего сообщения).
Перепишем выражения (3) и (4)
Указанное допущение «сломало» мне доказательство, которое я привел в сообщении от 5.03
-- 15 мар 2021 18:35 --Ещё соображение против такого доказательства: не видно где опираетесь на свойства простых близнецов, похоже таким методом можно "доказать" бесконечность почти любых комбинаций чисел, лишь бы они были взаимно простыми с большими праймориалами (вон заменили

и получили из одного другое). Как-то это чересчур сильное утверждение. ИМХО.
Я не понял, разобрались ли Вы в доказательстве бесконечности простых чисел, которое я привел в сообщении от 14.03? У меня к Вам вопрос-предложение по распределению взаимно простых чисел, которое озвучу в соседней теме.
Давайте, я Вам про близнецов расскажу позже.
-- 15 мар 2021 18:46 --И здесь я конкретно писал:
Проверив выражение для конкретных небольших примориалов , я обнаружил, что неравенство изредка не выполняется.
-- 15 мар 2021 19:01 -- Последний раз редактировалось Dmitriy40
15 мар 2021 17:09, всего редактировалось 2 раз(а).
Я о том что замена простой

на сумму начальной части ряда (ради регулярности ряда что ли?) выглядит не слишком полезной для рассуждения (и понимания).
Я просто указал место, где в выражении (14) находится

. ))