Ну это еще не приговор.
Проверка равномерности распределения вычетов для
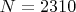
(примориал

) с длиной интервала
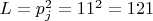
Модуль:
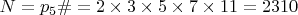
.
Функция Эйлера:
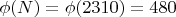
(количество вычетов, взаимно простых с

).
- Длина интервала:
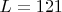
.
- Ожидаемое количество вычетов в интервале длины

:
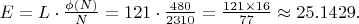
Результаты подсчёта для 10 последовательных интервалов длины 121:
Рассмотрены интервалы
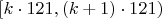
для
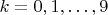
. Фактическое количество вычетов (

) и отклонение от

(т.е.
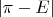
) подсчитаны программно. Результаты:
| Интервал (

) | Границы интервала | Фактическое количество вычетов (

) | Отклонение (
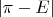
) |
|------------------|-------------------|-----------------------------------------|----------------------------|
| 0 |
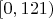
| 26 | 0.8571 |
| 1 |
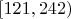
| 25 | 0.1429 |
| 2 |
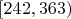
| 24 | 1.1429 |
| 3 |
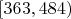
| 26 | 0.8571 |
| 4 |
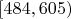
| 25 | 0.1429 |
| 5 |
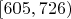
| 25 | 0.1429 |
| 6 |
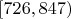
| 24 | 1.1429 |
| 7 |
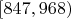
| 26 | 0.8571 |
| 8 |
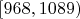
| 26 | 0.8571 |
| 9 |
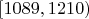
| 25 | 0.1429 |
Статистика отклонений:
- Минимальное отклонение:
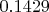
.
- Максимальное отклонение:
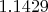
.
- Среднее абсолютное отклонение:
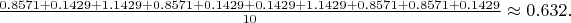
- Стандартное отклонение:
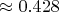
.
1. Фактические отклонения:
- Отклонения малы: все
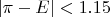
.
- Среднее отклонение
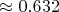
существенно меньше ожидаемого значения
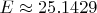
(относительная погрешность
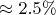
).
2. Сравнение с асимптотической оценкой Руста:
- Для
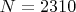
,
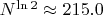
(где
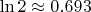
).
- Оценка ошибки:
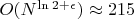
(для малого

).
- Фактические отклонения (
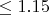
) значительно меньше оценки
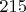
.
3. Причина расхождения:
- Условие
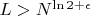
не выполняется:
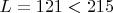
.
- Асимптотическая оценка
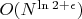
является верхней границей и может быть пессимистичной для конкретных

.
- Фактическое распределение вычетов более равномерно, чем предсказывает оценка, особенно для малых

.
Для
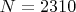
и
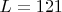
:
- Распределение вычетов практически равномерно: отклонения не превышают
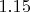
.
- Оценка
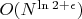
завышена (дает
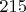
, реальные отклонения в

раз меньше).
- Это подтверждает, что асимптотическая оценка не оптимальна для малых

, но остается корректной (так как
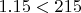
).
Для больших

(например,

) условие
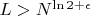
не выполняется, и оценка становится менее информативной. В таких случаях требуются более точные методы (например, гипотеза Римана).