Это для конкретного

, но отсюда не следует что оно останется верным для любых больших

: если количество простых близнецов таки ограничено, то когда-то станет
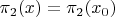
для всех

.
Имеем формулу расчета количества чисел, взаимно простых примориалу в этом же примориале:
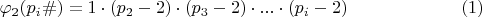
Чтобы определить плотность таких чисел в примориале, поделим на этот примориал:
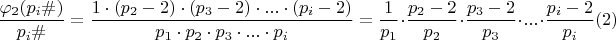
второе равенство в (2) возможно в виду мультипликативности функции
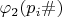
(3).
Умножив (2) на

и развернув его, получаем:
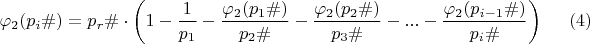
Допустим, имеется примориал

.
Определяем простое число

- ближайшее меньшее

. Тогда можно записать (4) для приморила

:
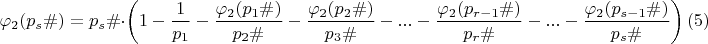
Перепишем (5) в несколько ином виде:
![$$\varphi_{2}(p_{s}\#)=p_s\#\cdot \left[\left(1-\dfrac {1}{p_{1}}-\dfrac {\varphi_{2}(p_{1}\#)}{p_{2}\#}-\dfrac {\varphi_{2}(p_{2}\#)}{p_{3}\#}-...-\dfrac {\varphi_{2}(p_{r-1}\#)}{p_{r}\#}\right)-\left(...+\dfrac {\varphi_{2}(p_{s-1}\#)}{p_{s}\#}\right)\right]\egno (6)$$ $$\varphi_{2}(p_{s}\#)=p_s\#\cdot \left[\left(1-\dfrac {1}{p_{1}}-\dfrac {\varphi_{2}(p_{1}\#)}{p_{2}\#}-\dfrac {\varphi_{2}(p_{2}\#)}{p_{3}\#}-...-\dfrac {\varphi_{2}(p_{r-1}\#)}{p_{r}\#}\right)-\left(...+\dfrac {\varphi_{2}(p_{s-1}\#)}{p_{s}\#}\right)\right]\egno (6)$$](https://dxdy-04.korotkov.co.uk/f/b/6/7/b6715b07f5c1107e2b58e75b9f1caf8f82.png)
Первая круглая скобка - это количество чисел, взаино простых с примориалом

, в примориале

. Вторая круглая скобка описывает количество чисел (от "действия" простых от

до

), на которое уменьшится количество первой скобки в примориале

.
Число в первой скобке существенно больше, чем число во второй.
Поэтому то, о чем Вы пишете, просто не может случиться.