Не

, а просто

. Соответственно здесь

, а не

.
Прошу извинить, но я очередной раз ошибся.
Имел в виду, что

- количество пар простых чисел-близнецов, не превышающих все же

.
Рассчитав по формуле (куда смог "дотянуться")
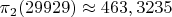
при фактическом значении

, я решил, что мои значения далее будут только приближаться к фактическим, причем снизу. Но расчеты, которые привел
Dmitriy40, опровергли мое предположение.
Я не задавался целью составления точной формулы расчета, а лишь хотел привести формулу с хорошим приближением (если бы таковая нашлась) в качестве дополнительного аргумента к способу доказательства бесконечности простых чисел-близнецов, суть которого заключается в следующем:
Так как простые числа бесконечны, то и примориалы этих чисел бесконечны, соответственно, бесконечен рост количества пар взимно простых к этому примориалу чисел-близнецов до
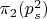
, где пары взаимно простых чисел-близнецов являются парами простых чисел-близнецов.
При этом функция
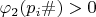
.
(Оффтоп)

- мультипликативная функция, значение которой равно* количеству пар близнецов (натуральных чисел с разницей

), не превышающих

и в которых оба числа взаимно простые с

("пары, взаимно простых с

"). Для каждого простого числа

функция

, кроме простого числа

, для которого

.
Функция

позволяет удалить два вычета из кольца вычетов простого числа.
В данном рассмотрении производится проверка пар натуральных чисел на выполнение сравнения:

(где

- натуральные числа от

до

) и удаление таких пар из числа пар, взаимно простых с

, т.е. подразумевается удаление двух остатков:

.