Распределение взаимнопростых чисел в примориалах.

[Yadryara]

Да не так уж важно, просто интересно, неужели даже такие не сильно сложные расчёты Вам не доступны?

Не будем показывать пальцем, но кое-кто и в 75 лет с подобным счётом управляется.

Вы скажите: в чём конкретно сложности? Могу попробовать пошагово объяснить как считать такие вещи самостоятельно.

[Батороев]

Yadryara
Не сомневаюь, что есть пожилые люди, которые занимаются расчетами. Но скорее всего, они освоили программы немного ранее.
Откровенно говоря, кроме указанного мной хобби (ковыряться в ТЧ), у меня есть еще - музыка, которой тоже увлекаюсь.
До с.г. меня довольно часто приглашали поучаствовать в проектах по старому месту работы. Сейчас я наотрез отказался.
Еще есть технические идеи, скопившиеся по жизни.Некоторые сейчас прорабатываю.

[Dmitriy40]

Самое сложное в расчётах таблицы было посчитать интеграл. Что умеет делать как вольфрамальфа, так и банальный эксель (уверен, не пробовал). Остальные числа взяты просто из OEIS готовыми. Так что никаких сложных программ осваивать не нужно, уж найти как посчитать интеграл в экселе и в вольфрамальфе можно за полчаса.
Вот сможет ли эксель посчитать константу $W$ с хорошей точностью (более 3-5 знаков) не уверен, может и обломается (кажется он очень медленно работает с простыми числами). Но для оценки погрешностей хватит и 3-4 знака $W$.

[Батороев]

Dmitriy40
Еще раз благодарю за расчеты!
Для "самопальной" формулы этого вполне достаточно. Я не стремился к созданию объективно точной формулы. Как Вы наверное заметили, у меня все выкладки пестрят знаками "$\approx$".
Мне даже нравится, что проценты - все отрицательные и, не смотря на Ваше замечание:

Dmitriy40 в сообщении #1692235 писал(а):

а дальше точность почти не улучшается.

она в процентном отношении, хоть и медленно, но все же повышается, причем неуклонно.

[Батороев]

Возвращаясь к теме...

Есть дробь:

$$ \dfrac {\varphi (p_i\#)}{p_{i}\#}=\dfrac {(2-1)\cdot (3-1)\cdot (5-1)...(p_i-1)}{2\cdot 3\cdot 5... p_i}\eqno (1) $$

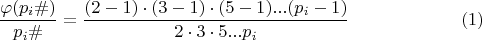
где $\varphi (p_i\#)$ - функция Эйлера для примориала $p_i\#$
В этой дроби можно сокращать числитель и знаменатель на общие множители, а соответственно - на их произведения.
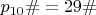
Например, для примориала $p_{10}\#=29\#$ такими общими множителями являются числа: $2,3,5,7,11$
При сокращении числителя и знаменателя дроби (1) на общие множители мы получаем равные участки примориала с равным количеством чисел, взаимно простых этому примориалу.

Кроме того, существует (так называемая мной) "Теорема Руст'а", которая утверждает, что числитель и знаменатель дроби (1) можно делить на $2^{i-1}$.

-- 30 июл 2025 16:42 --

Руст в сообщении #625700 писал(а):

Доказательство: Каждому вычету х сопоставим координаты $x=\sum_{j\le i}x_jN_j\mod N$, где $N=\prod_{j\le i}p_j=p_i\#, N_j=\frac{N}{p_j}$. Любые ненулевые координаты $1\le x_j<p_j$ определяет один вычет $x$, взаимно простой с $N$.
При этом если зафиксируем одну из координат, то получаем вычеты по модулю $N_j$. По индукции вычеты по модулю $N_j$ удовлетворяют этому свойству при любом $j$, т.е. каждый из $2^{i-2}$ интервалов длины $L_j$ имеет ровно $M_j=2^{2-i}\prod_{k\not =j}(p_k-1)$ вычетов и докажем это свойство по модулю $N$. Длина рассматриваемых интервалов по модулю $N_j$ есть $L_j=\frac{N_j}{2^{i-2}}$, а по модулю $N$ есть $L=\frac{N}{2^{i-1}}=L_j\frac{p_j}{2}.$
Учитывая симметрию $x_j\to p_j-x_j$ получаем, что объединенные $p_j$ интервалов длины $L_j$ обладают симметрией и поэтому каждый из интервалов длины $L$ имеет ровно $\frac{p_j-1}{2}M_j=2^{1-i}\prod_{k\le i}(p_k-1)$ вычетов.

Отсюда получается почти равномерность ПСВ, т.е. в интервале $(A,B), B-A>N^{ln2 +\epsilon}$ содержится вычетов $\pi(A,B)=(B-A)\prod_j(1-\frac{1}{p_j})+O(N^{\ln 2+\epsilon})$ (для хорошей равномерности не хватает то, что $\ln 2>0.5)$.

[Soul Friend]

то есть по "теореме Руст'а" считаем $\prod_{i>2} (\frac{p_i-1}{2})$ ?

но не для всех $\frac{P_n - 1}{2^{x_n}} = q$ $q$ - простое число.

[Батороев]

Soul Friend
Здесь речь идет только о расчете количества взаимно простых (не простых) чисел.

[vicvolf]

Батороев в сообщении #1695929 писал(а):

Soul Friend Здесь речь идет только о расчете количества взаимно простых (не простых) чисел.

Из так называемой теоремы Руста следует:

Руст в сообщении #625700 писал(а):

Отсюда получается почти равномерность ПСВ, т.е. в интервале $(A,B), B-A>N^{ln2 +\epsilon}$ содержится вычетов $\pi(A,B)=(B-A)\prod_j(1-\frac{1}{p_j})+O(N^{\ln 2+\epsilon})$

Эта равномерность распространяется на любой интервал ПСВ_$p_j$#. Следовательно, также на интервал от $p_{j+1}$ до ${p_j}^2$, где находятся одни простые числа. Однако, у меня есть сомнения в этом доказательстве.

[Батороев]

vicvolf в сообщении #1695973 писал(а):

Эта равномерность распространяется на любой интервал ПСВ_$p_j$#. Следовательно, также на интервал от $p_{j+1}$ до ${p_j}^2$, где находятся одни простые числа. Однако, у меня есть сомнения в этом доказательстве.

Вы верно угадали главную идею моего предыдущего сообщения.
Только у меня было желание для расчета числа простых, разбить примориал до интервала от $1$ до $p_{i}^2$, после чего из числа полученных на этом участке взаимно простых вычесть единицу (число $1$ для всех примориалов является взаимно простым) и добавить $i$.
Теорему Руст'а я, как мог, прверял. Вроде бы, все сходится.
Одна беда - ни степени $2$-ки, ни общие множители числителя и знаменателя не позволяют для достаточно больших примориалов разбить их до искомых величин.
Надо еще что-то искать.

[vicvolf]

Батороев в сообщении #1695840 писал(а):

Кроме того, существует (так называемая мной) "Теорема Руст'а", которая утверждает, что числитель и знаменатель дроби (1) можно делить на $2^{i-1}$.

Распределение вычетов, взаимно простых с $N = p_3\# = 30$(т.е. чисел, не делящихся на 2, 3, 5), по интервалам длины $L = \frac{N}{2^{i-1}} = \frac{30}{4} = 7.5$ не является равномерным. Контрпример опровергает исходное утверждение о строгой равномерности. Детали:

Список всех вычетов, взаимно простых с 30:
$\boxed{1,\ 7,\ 11,\ 13,\ 17,\ 19,\ 23,\ 29} \quad (\text{всего } \phi(30) = 8 \text{ вычетов}).$

Разбиение интервала $[1, 30]$ на 4 интервала длины 7.5:
1. $[1, 8.5)$:
Целые числа: $1, 2, \dots, 8$.
Взаимно простые с 30: $\boxed{1},\ \boxed{7}$→ 2 вычета.

2. $[8.5, 16)$:
Целые числа: $9, 10, \dots, 15$.
Взаимно простые с 30: $\boxed{11},\ \boxed{13}$→ 2 вычета.

3. $[16, 23.5)$:
Целые числа: $16, 17, \dots, 23$.
Взаимно простые с 30: $\boxed{17},\ \boxed{19},\ \boxed{23}$→ 3 вычета.

4. $[23.5, 30]$:
Целые числа: $24, 25, \dots, 30$.
Взаимно простые с 30: $\boxed{29}$→ 1 вычет.

[Батороев]

vicvolf
Имеем 4 интервала:
$1..7,5
$7,5..15
$15..22,5$
$22,5..30$

[vicvolf]

Батороев Начнем с того, что не получается разделить на равные интервалы по 7,5. У Вас первый интервал длиной 6,5, а у меня последний.

[Батороев]

vicvolf
Я должен был записать первый интервал точнее: $0..7,5$.

[Батороев]

Батороев в сообщении #1696023 писал(а):

Одна беда - ни степени $2$-ки, ни общие множители числителя и знаменателя не позволяют для достаточно больших примориалов разбить их до искомых величин.

Сдается мне, что здесь я не прав... Скорость роста произведения общих множителей числителя и знаменателя дроби (1) значительно выше, чем я ранее считал.

[vicvolf]

Батороев
Да, строгая равномерность наблюдается только для специального разбиения (начинающегося с 0 и основанного на системе координат). Я проверил это на другом примере.

Проверка равномерности распределения для $N = 210$
При $N = p_4\# = 210$(где $p_1=2, p_2=3, p_3=5, p_4=7$, число интервалов определяется как $2^{i-1} = 2^{3} = 8$, а длина интервала:
$L = \frac{N}{2^{i-1}} = \frac{210}{8} = 26.25.$

Ожидаемое количество вычетов (чисел, взаимно простых с 210) на интервал:
$M = 2^{1-i} \prod_{k \leq i} (p_k-1) = \frac{1}{8} \cdot (1 \cdot 2 \cdot 4 \cdot 6) = \frac{48}{8} = 6.$

Распределение вычетов по интервалам $[0, 210]$
Общее количество вычетов: $\phi(210) = 48$.
Разобьём $[0, 210]$ на 8 интервалов длины $L = 26.25$:

1. $[0, 26.25)$:
Целые числа: $1, 2, \dots, 26$.
Взаимно простые с 210:
$ \boxed{1},\ \boxed{11},\ \boxed{13},\ \boxed{17},\ \boxed{19},\ \boxed{23} \quad \text{(6 вычетов)}. $

2. $[26.25, 52.5)$:
Целые числа: $27, 28, \dots, 52$.
Взаимно простые с 210:
$ \boxed{29},\ \boxed{31},\ \boxed{37},\ \boxed{41},\ \boxed{43},\ \boxed{47} \quad \text{(6 вычетов)}. $

3. $[52.5, 78.75)$:
Целые числа: $53, 54, \dots, 78$.
Взаимно простые с 210:
$ \boxed{53},\ \boxed{59},\ \boxed{61},\ \boxed{67},\ \boxed{71},\ \boxed{73} \quad \text{(6 вычетов)}. $

4. $[78.75, 105)$:
Целые числа: $79, 80, \dots, 104$.
Взаимно простые с 210:
$ \boxed{79},\ \boxed{83},\ \boxed{89},\ \boxed{97},\ \boxed{101},\ \boxed{103} \quad \text{(6 вычетов)}. $

5. $[105, 131.25)$:
Целые числа: $105, 106, \dots, 131$.
Взаимно простые с 210:
$ \boxed{107},\ \boxed{109},\ \boxed{113},\ \boxed{121},\ \boxed{127},\ \boxed{131} \quad \text{(6 вычетов)}. $

6. $[131.25, 157.5)$:
Целые числа: $132, 133, \dots, 157$.
Взаимно простые с 210:
$ \boxed{137},\ \boxed{139},\ \boxed{143},\ \boxed{149},\ \boxed{151},\ \boxed{157} \quad \text{(6 вычетов)}. $

7. $[157.5, 183.75)$:
Целые числа: $158, 159, \dots, 183$.
Взаимно простые с 210:
$ \boxed{163},\ \boxed{167},\ \boxed{169},\ \boxed{173},\ \boxed{179},\ \boxed{181} \quad \text{(6 вычетов)}. $

8. $[183.75, 210]$:
Целые числа: $184, 185, \dots, 209$.
Взаимно простые с 210:
$ \boxed{187},\ \boxed{191},\ \boxed{193},\ \boxed{197},\ \boxed{199},\ \boxed{209} \quad \text{(6 вычетов)}. $

Однако это частный случай. При сдвиге границ интервалов равномерность нарушается.
Критическая длина для "почти равномерности"
Исходное утверждение о почти равномерности справедливо для интервалов длины $B - A > N^{\ln 2 + \epsilon}$. Для $N = 210$:
$N^{\ln 2} = 210^{0.693} \approx 40.7, \quad \text{где } \epsilon > 0.$
Интервалы длины $L = 26.25 < 40.7$ могут проявлять отклонения (как в примере со сдвигом).
- При $B - A > 40.7$ отклонения становятся малыми:
$ \pi(A, B) = (B - A) \cdot \prod_{j} \left(1 - \frac{1}{p_j}\right) + O(N^{\ln 2 + \epsilon}). $

Позже приведу пример с такими интервалами.