Доказать несчётность отрезка теоремой Бэра

[cxzbsdhwert]

tolstopuz в сообщении #1713613 писал(а):

cxzbsdhwert в сообщении #1713612 писал(а):

Я пытался понять, на основании чего одного следствие ставилось выше другого. Другое просто игнорировалось.

Для любой причины можно придумать бесконечное множество следствий. Как называл это Борхес, "сад расходящихся тропок". Выбирается та тропка, которая ведет к желаемому результату, в данном случае верному доказательству.

Тогда истинность зависит от желания, а это не так.

Да, наверное у причины может быть много следствий. Тогда наверное причина истинна если истинны все следствия. Или может у каждой причины есть ложные следствия и не в этом дело? Не знаю, я уже запутался

[skobar]

(Оффтоп)

tolstopuz в сообщении #1713613 писал(а):

Для любой причины можно придумать бесконечное множество следствий. Как называл это Борхес, "сад расходящихся тропок". Выбирается та тропка, которая ведет к желаемому результату, в данном случае верному доказательству.

Все идет по кругу, и это уже писалось:

skobar в сообщении #1713383 писал(а):

3. В качестве следствия из $(1)$ имеем следующее разбиение

$$[a,b]=\bigcup_n \ \{x_n\} $$

Я подчеркиваю, что это разбиение - это следствие отрицания. Из отрицания доказываемого утверждения можно вывести много следствий (множество различных разбиений), но мы выбираем именно такое. Мы не можем выбирать отрицание к доказываемому утверждению, потому что оно одно, но мы можем выбрать любое следствие из отрицания.

Этот круг не приводит к просветлению TC

[Mikhail_K]

cxzbsdhwert в сообщении #1713616 писал(а):

Тогда истинность зависит от желания, а это не так.

Не зависит от желания. Какую бы тропку мы ни выбрали, мы не сможем прийти к неверным выводам. При выборе любой тропки мы будем получать только верные выводы, но большинство тропок приведут к бесполезным и неинтересным для нас выводам (хотя тоже верным), и лишь небольшое количество тропок приведут к тем верным выводам, которые нас интересуют.

-- 29.12.2025, 21:11 --

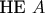
Ещё. Пусть мы доказываем от противного утверждение $A$ и для этого предполагаем отрицание ${\textrm{НЕ}}\,\,A$. Из него мы делаем разные выводы - с помощью одной теоремы, с помощью другой теоремы, используя одни разбиения, используя другие разбиения. При многих таких способах рассуждения мы не получим противоречия - но это не будет ничего означать. Но если найдётся хотя бы один способ рассуждения, при котором мы придём к противоречию, то тем самым $A$ будет доказано - вне зависимости от того, ведут ли куда-то другие способы.

Очень многие математики пытались доказать от противного теорему Ферма. У большинства из них это не получилось. Это не значит, что они обязательно допускали какие-то ошибки. Опираясь на неверное утверждение и делая из него выводы, мы можем получить противоречие, но можем и не получить - особенно если используем не те инструменты (например, не те теоремы или не те разбиения). Но если какая-то одна ветвь рассуждений привела к противоречию - то всё, цель достигнута.

[cxzbsdhwert]

Mikhail_K в сообщении #1713618 писал(а):

cxzbsdhwert в сообщении #1713616 писал(а):

Тогда истинность зависит от желания, а это не так.

Не зависит от желания. Какую бы тропку мы ни выбрали, мы не сможем прийти к неверным выводам. При выборе любой тропки мы будем получать только верные выводы, но большинство тропок приведут к бесполезным и неинтересным для нас выводам (хотя тоже верным), и лишь небольшое количество тропок приведут к тем верным выводам, которые нас интересуют.

Нет, именно желания, поскольку Вы сами пишите что идёте к выводу "верному" - а это понятие субъективное.

Мы обсуждаем конкретные объективные вещи - причина и наличие у неё множества следствий. Причина ложна если ложно следствие. Но какова истинность причины, если есть два следствия из неё, одно из которых ложно, а другое истинно? Вот в чём вопрос.

[Mikhail_K]

cxzbsdhwert в сообщении #1713619 писал(а):

Причина ложна если ложно следствие.

Да.

cxzbsdhwert в сообщении #1713619 писал(а):

Но какова истинность причины, если есть два следствия из неё, одно из которых ложно, а другое истинно?

В этом случае причина ложна.

Например, из утверждения $1=-1$ можно получить неверное следствие $1+1=-1+1$ то есть $2=0$, а можно получить верное следствие $1^2=(-1)^2$ то есть $1=1$. Нашлось хотя бы одно неверное следствие - значит, посылка ложна. Но у неверного утверждения могут быть и верные следствия, не приводящие к противоречиям.

cxzbsdhwert в сообщении #1713619 писал(а):

Вот в чём вопрос.

Это азы математической логики.
Посмотрите ещё моё предыдущее сообщение, я там его дописал, чтобы было ещё понятнее.

[cxzbsdhwert]

Mikhail_K в сообщении #1713620 писал(а):

cxzbsdhwert в сообщении #1713619 писал(а):

Но какова истинность причины, если есть два следствия из неё, одно из которых ложно, а другое истинно?

В этом случае причина ложна.

Не можем ли мы предъявить явно истинную причину из которой всё также будут как ложные так и истинные следствия?

[skobar]

cxzbsdhwert
Все-таки ответьте, пожалуйста, на вопрос:

skobar в сообщении #1713611 писал(а):

Можете четко сформулировать, что должно быть задано, чтобы были созданы условия, в которых можно применять теорему Бэра

Это важно, так как похоже, что именно этот (ключевой) момент вы понимаете неправильно.

[cxzbsdhwert]

skobar
Да я Вас не игнорирую, и спасибо ещё раз что уделяете время.

По словам Лектора: должно быть непустое замкнутое множество $F$, "представленное как" объединение нбчс набора замкнутых множеств.

[skobar]

cxzbsdhwert в сообщении #1713622 писал(а):

Не можем ли мы предъявить явно истинную причину из которой всё также будут как ложные так и истинные следствия?

Не можем. Из истинного утверждения следуют только истинные. Это азы математической логики.

-- 29.12.2025, 21:32 --

cxzbsdhwert в сообщении #1713624 писал(а):

skobar
Да я Вас не игнорирую, и спасибо ещё раз что уделяете время.
По словам Лектора: должно быть непустое замкнутое множество $F$, "представленное как" объединение нбчс набора замкнутых множеств.

Как видите, чтобы применять теорему Бэра должны уже быть две вещи:
1) Замкнутое множество $F$
2) Не более чем счетное семейство замкнутых множеств $F_1, F_2, \dots$, которые в объединении дают $F$. Подчеркиваю, что это какое-то одно семейство, которое уже выбрано.
То есть мы сначала выбираем какое-то представление $F$ в виде объединения замкнутых множеств, и только потом применяем теорему Бэра к этому одному конкретному представлению. Вы же пытаетесь применять теорему Бэра сразу ко многим представлениям $F$. Это так не работает. Сначала выбор представления в виде объединения замкнутых множеств, и только потом применение теоремы Бэра к этому представлению. Утром деньги, вечером стулья, но не наоборот.

[cxzbsdhwert]

skobar в сообщении #1713625 писал(а):

cxzbsdhwert в сообщении #1713622 писал(а):

Не можем ли мы предъявить явно истинную причину из которой всё также будут как ложные так и истинные следствия?

Не можем. Из истинного утверждения следуют только истинные. Это азы математической логики.

Но в то же время, следствия могут находиться в другом логическом отношении.

Для нашего случая мы показали что следствия образуют конъюнкцию:

если отрезок нбчс то (существует ... И существует...)

Но ранее я использовал следствия с другими кванторами (или предикатами), которые находились в отношении дизъюнкции:

если отрезок нбчс то (представлен только одноточечным объединением ИЛИ представлен не только одноточечным объединением)

И это тоже следствие. Ну видимо раз я написал "И" "это тоже следствие", тогда, что получается-то? :

если отрезок нбчс то ((существует ... И существует ...) И (представлен в ... ИЛИ представлен в ...))

И тогда для ложности всего следствия достаточно ложности только одного из "существует"

[Mikhail_K]

cxzbsdhwert, начинаете мыслить в верном направлении. Из любого утверждения можно сделать сколько угодно разных выводов, и если угодно, то их можно записать все через "И". Но достаточно показать ложность только одного из них, и тогда будет доказана ложность исходного утверждения. Потому что, будь исходное утверждение истинным, из него не удалось бы получить ни одного ложного вывода. Из истины следует только истина, а из лжи следует что угодно.

[cxzbsdhwert]

Mikhail_K в сообщении #1713629 писал(а):

cxzbsdhwert, начинаете мыслить в верном направлении. Из любого утверждения можно сделать сколько угодно разных выводов, и если угодно, то их можно записать все через "И". Но достаточно показать ложность только одного из них, и тогда будет доказана ложность исходного утверждения. Потому что, будь исходное утверждение истинным, из него не удалось бы получить ни одного ложного вывода. Из истины следует только истина, а из лжи следует что угодно.

А есть строгое объяснение почему с "существует" конъюнкция, а не дизъюнкция?

Почему с "представлен" не конъюнкция понятно. Потому что "представлен" это вообще прошедшее законченное время, то есть уже представлен. И если уже представлен, то не может быть и одноточечным и не одноточечным, поэтому только или.

[Mikhail_K]

cxzbsdhwert в сообщении #1713630 писал(а):

А есть строгое объяснение почему с "существует" конъюнкция, а не дизъюнкция?

Потому что отдельно можно получить вывод о существовании одноточечных разбиений и отдельно можно получить вывод о существовании неодноточечных разбиений (как именно - говорилось выше). Значит, можно получить и их конъюнкцию - фактически по определению этой самой конъюнкции. Ну или если Вам хочется углубиться на самый фундаментальный уровень, как всё обосновывать с опорой на логические аксиомы и правила вывода - то читайте
Мендельсон. Введение в математическую логику
Верещагин, Шень. Языки и исчисления
Другое дело, что конъюнкция тут не нужна, достаточно вывода про одноточечное разбиение. И импликация с одним таким выводом, без конъюнкций, также справедлива.

cxzbsdhwert в сообщении #1713630 писал(а):

Почему с "представлен"

Слова "представлен" в корректных математических записях быть вообще не должно. Я об этом выше говорил: можно писать "представим", а не "представлен". Потому что математические утверждения должны выражать свойства математических объектов, а не того, как эти объекты записаны (представлены).

[skobar]

Mikhail_K в сообщении #1713631 писал(а):

Слова "представлен" в корректных математических записях быть вообще не должно. Я об этом выше говорил: можно писать "представим", а не "представлен". Потому что математические утверждения должны выражать свойства математических объектов, а не того, как эти объекты записаны (представлены).

В смысле "слова "представлен" в корректных математических записях быть вообще не должно"? Могут быть и "представим", и "представлен" - с разными смыслами.

В обсуждаемом следствии из теоремы Бэра как раз правильно писать, что множество $F$ "представлено" в виде объединения, а не "представимо".

[Mikhail_K]

skobar
Ну, ТС пишет такое утверждение: "Если отрезок нбчс, то он представлен в виде объединения нбчс набора одноточечных множеств или в виде объединения нбчс набора неодноточечных множеств". И считает, что если отрезок "представлен" в одном виде (это, мол, прошедшее время, уже совершилось) - то, значит, не представлен в другом виде. Это, понятное дело, неверно (или просто не переводится на корректный математический язык, если тут имеются в виду суждения не об отрезке, а о записи). И чтобы не было этой путаницы, лучше от слова вообще на первых порах отказаться.

Я соглашусь, что некоторые математические утверждения может быть удобно переводить на язык слов с использованием слова "представлен". Хотя без этого слова всегда можно обойтись, чтобы не получалось путаницы как у ТС здесь.