Почему только сомнения?
Теорема Бэра, имеет такую логическую структуру: для каждой "фигни" выполняется "утверждение".
По правилам математической логики отрицание этой теоремы имеет такую структуру: существует (хотя бы одна такая) "фигня", для которой (это самое) "утверждение" не выполняется.
То есть, достаточно найти одну "фигню", а рассматривать другие нет надобности.
Вы разницу между "существует" и "для каждого" понимаете?
В этом и проблема, поскольку, по крайней мере в той формулировке, в которой её дал Лектор, и в которой мы её обсуждали, Теорема не очень похожа на утверждение вида "для каждого

истинно

":
"Пусть

непустое замкнутое подмножество и

"представлено как" объединение нбчс набора замкнутых множеств. Тогда ..."
Это больше похоже на импликацию "если

то

", но я так понимаю, "если" как раз сводится к кванторам "для любого И такого что".
Тут пишут что "пусть" вообще сложно назвать квантором, и предлагают заменять его на "всякий", поэтому ок.
Но дело главным образом в формулировке, пусть даже с "если" - "если представлено в виде".
Так вот, я настаивал на том, что

"представленным в виде" выражения "объединение только одноточечных множеств" И выражения "объединения не только одноточечных множеств" быть не может.

может быть представлено в виде ИЛИ такого ИЛИ такого выражения, но не их обоих одновременно.
Тогда получается вот что:
1. Отрезок несчётен. Отрицание - "отрезок не более чем счётен(нбчс)" ("существует счетный отрезок", хотя я тут тоже не очень согласен, мы же обсуждаем отрезок как вид).
2. Если отрезок нбчс, то он представлен как объединение нбчс набора только одноточечных множеств ИЛИ представлен как объединение не только одноточечных.
3. Дальше, чтобы показать ложность причины - "всякий отрезок не более чем счётен" по правилу импликации нужно показать ложность следствия - "он представлен как (... ИЛИ ...)".
4. Лектором показывается противоречие одноточечного случая, то есть: по теорема Бэра для всякого нбчс (замкнутого) множества представленного в виде объединения нбчс набора одноточечных множеств найдётся интервал пересечение которого со всем множеством лежит в одном из одноточечных. А по определению отрезка пересечение состоит из более чем одной точки. Противоречие.
5. Но противоречие только одноточечного случая не означает ложности следствия, поскольку следствие - дизъюнкция. Необходима ложность и не одноточечного случая.
Почему я настаиваю на том, что "представлено как" не тоже самое что "равно" - потому что в Теореме Бэра роль играет выражение, которым представляется

, а не значение это выражения.
Если нам важно только значение, то мы говорим о равенстве выражений

и

. Если нам важны сами выражения, например мы сравниваем многочлены по числу членов, то

и

это разные выражения, и делать выводы о числе слагаемых

по числу слагаемых

, лишь на основании того что они равны не верно. То есть не верно утверждать что

это одночлен, поскольку он равен семи, ну а "семь" это же одночлен.
Не верно утверждать что
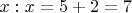
это одночлен И многочлен. Верно утверждать, что
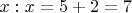
это одночлен ИЛИ многочлен.
warlock66613Кстати формулировку "представлено как объединение" дословно всё-таки
привёл Лектор, формулируя теорему
-- 29.12.2025, 15:50 --SomeoneНу то есть, кратко:
1. Утверждается, что любой отрезок несчётен.
2. От обратного - существует нбчс отрезок (не противоречащий Теореме Бэра). То есть достаточно предъявить нбчс отрезок, так чтобы не возникало противоречия (для начала с Теоремой Бэра. Дальше всё равно возникнет, но не с Теоремой Бэра).
3. Ну вот, предъявлен - нбчс отрезок "представленный как" объединение нбчс набора неодноточечных множеств. С Теоремой Бэра и тем фактом, что пересечение интервала с отрезком имеет более одной точки противоречия не возникло.