Доказать несчётность отрезка теоремой Бэра

[skobar]

Mikhail_K в сообщении #1713635 писал(а):

Ну, ТС пишет такое утверждение: "Если отрезок нбчс, то он представлен в виде объединения нбчс набора одноточечных множеств или в виде объединения нбчс набора неодноточечных множеств".
Я говорю, что "представлен" тут непонятно что значит, не переводится на строгий математический язык, так как это утверждение не об отрезке, а о его записи. Со словом "представим" утверждение было бы понятным, и можно было бы использовать "и", а не только "или".

В таком контексте да, здесь требуется слово "представим".

Mikhail_K в сообщении #1713635 писал(а):

Вот что важно: нет такого математического утверждения "множество $A$ представлено в таком-то виде", но есть утверждение "множество $A$ представимо в таком-то виде".

Мне видится, что есть и то, и другое утверждение, но смысл немного разный. В первом случае (уже) задано какое-то представление множества $A$, а во втором говорится, что множество $A$ можно представить в каком-то виде.

Обсуждаемое здесь следствие теоремы Бэра формулируется так (один из возможных вариантов):
"Пусть $F$ - замкнутое множество, представленное в виде не более чем счетного семейства замкнутых множеств $F=\cup_n F_n$, тогда ..."
Если здесь слово "представленное" заменить на "представимое", то меняется смысл и теряется корректная формулировка теоремы.

Кстати, то, что ТС использовал контекст, в котором правильнее употреблять слово "представимо", imho связано c его неправильным пониманием формулировки теоремы (что и послужило причиной задать ему вопрос выше). Правильным был бы контекст, где уместно слово "представлено".

[Mikhail_K]

Подумал, какой всё-таки смысл можно придать утверждению ТС "Если отрезок нбчс, то он представлен в виде объединения нбчс набора одноточечных множеств или в виде объединения нбчс набора неодноточечных множеств" (если тут именно слово "представлен", а не "представим"). Можно сказать "Если $F=\bigcup\limits_{n=1}^\infty F_n$, то все $F_n$ одноточечные или не все $F_n$ одноточечные" - и это будет корректное утверждение. А утверждение "Если $F=\bigcup\limits_{n=1}^\infty F_n$, то все $F_n$ одноточечные или все $F_n$ неодноточечные" - тоже корректное, но уже неверное. Это имел в виду ТС или не это, не знаю; но по-любому в таком виде, без слова "представлен", оно понятнее. И, конечно, в этом виде утверждение для обсуждаемого рассуждения не нужно.

Для рассуждения нужна представимость $F$ в виде объединения нбчс набора одноточечных множеств: существуют такие одноточечные $F_n$, что $F=\bigcup\limits_{n=1}^\infty F_n$. Представимость $F$ в виде объединения нбчс набора неодноточечных множеств тоже справедлива, но для рассуждения не нужна.

Для ТС: со skobar у нас нет никакого спора по существу - и он и я всё понимаем правильно, просто используем разные слова.
У ТС использование слова "представлен" ведёт к ошибкам, и поэтому я не советую его использовать. Без него можно обойтись.

[skobar]

Mikhail_K в сообщении #1713637 писал(а):

У ТС использование слова "представлен" ведёт к ошибкам, и я не советую ТС его использовать.

Немножечко не так :) Все сложнее:

skobar в сообщении #1713636 писал(а):

Использование ТС контекста, в котором правильнее употреблять слово "представимо", imho связано c его неправильным пониманием формулировки теоремы (что и послужило причиной задать ему вопрос выше). Правильным был бы контекст, где уместно слово "представлено".

[Mikhail_K]

skobar
Думаю, Вы согласитесь со мной, если я посоветую ТС переводить слова (хоть "представлен", хоть "представим", хоть другие подобные) на язык формул и кванторов. И собеседникам ТС тоже это посоветую. Путаницы из-за неодинакового понимания слов точно станет меньше.

[Someone]

(gipokrat)

gipokrat в сообщении #1713574 писал(а):

Someone в сообщении #1712490 писал(а):

kirillovw в сообщении #1712474 писал(а):

Мне не нравится, что доказательство через контрпример не дает ответа на вопрос "почему".

Потому что существует контрпример.
...

Мне тоже не нравится такой расклад.
Представьте себе:

— Почему не все люди имеют рост ниже двух метров?
— Потому что есть контрпример.

Серьёзно? Это и есть объяснение причины?

Да. Вы ищете "физическую" причину. В математике нет "физических" причин, есть только логические. А логической причиной в данном случае является именно наличие контрпримера.

cxzbsdhwert в сообщении #1713565 писал(а):

Someone в сообщении #1713559 писал(а):

Почему только сомнения?
Теорема Бэра, имеет такую логическую структуру: для каждой "фигни" выполняется "утверждение".
По правилам математической логики отрицание этой теоремы имеет такую структуру: существует (хотя бы одна такая) "фигня", для которой (это самое) "утверждение" не выполняется.
То есть, достаточно найти одну "фигню", а рассматривать другие нет надобности.

Вы разницу между "существует" и "для каждого" понимаете?

В этом и проблема, поскольку, по крайней мере в той формулировке, в которой её дал Лектор, и в которой мы её обсуждали, Теорема не очень похожа на утверждение вида "для каждого $x$ истинно $P(x)$":
"Пусть $F$ непустое замкнутое подмножество и $F$ "представлено как" объединение нбчс набора замкнутых множеств. Тогда ..."

Вы, к сожалению, очень плохо понимаете математический текст. Лектор сформулировал теорему в достаточно вольном стиле. У меня эта формулировка сразу транслируется в такую:
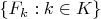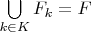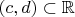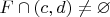Теорема. Пусть $F$ — непустое замкнутое подмножество множества действительных чисел $\mathbb R$. Тогда для любого не более чем счётного набора $\{F_k:k\in K\}$ замкнутых подмножеств $\mathbb R$, удовлетворяющего условию $\bigcup\limits_{k\in K}F_k=F$, существует такой интервал $(c,d)\subset\mathbb R$, что $F\cap(c,d)\neq\varnothing$, и существует такое $k\in K$, что $F\cap(c,d)\subseteq F$.

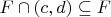Формулировка теоремы состоит из условия и заключения. Условием в данном случае является предположение "Пусть $F$ — непустое замкнутое подмножество множества действительных чисел $\mathbb R$." А всё остальное — заключение, которое имеет как раз такую структуру, как я написал. 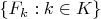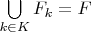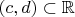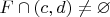Причём, "фигня" — это "не более чем счётный набор $\{F_k:k\in K\}$ замкнутых подмножеств $\mathbb R$, удовлетворяющий условию $\bigcup\limits_{k\in K}F_k=F$", а "утверждение" — это "существует такой интервал $(c,d)\subset\mathbb R$, что $F\cap(c,d)\neq\varnothing$, и существует такое $k\in K$, что $F\cap(c,d)\subseteq F$."

cxzbsdhwert в сообщении #1713612 писал(а):

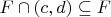Хорошо, и тем самым Вы неявно согласились с тем, что у вышеуказанной причины есть более одного следствия.

Потрясающее открытие! Оказывается, у одного утверждения может быть много следствий! А мы-то, профессиональные математики, и не знали об этом… Вы нам прямо глаза открыли.

cxzbsdhwert в сообщении #1713612 писал(а):

Если отрезок нбчс - то существует одноточечное ...
Если отрезок нбчс - то существует не одноточечное ...

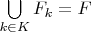
Разумеется. В равенстве $\bigcup\limits_{k\in K}F_k=F$ множества $F_k$ могут иметь любую мощность, не превосходящую мощности отрезка.

cxzbsdhwert в сообщении #1713612 писал(а):

Я пытался понять, на основании чего одного следствие ставилось выше другого. Другое просто игнорировалось.

Никто ничего не "ставит выше". Если я строю доказательство, то я использую для этого именно те блоки, которые считаю нужным. Если я выберу неудачные блоки, то моя постройка развалится.

Кстати, в обсуждаемом доказательстве несчётности можно использовать множества $F_k$ любой конечной мощности, и даже не обязательно одинаковой у всех или хотя бы ограниченной каким-то натуральным числом. Доказательство благополучно пройдёт, потому что, если отрезок и интервал пересекаются, то в их пересечении нетрудно указать любое конечное число точек. И одну, и две, и двадцать две, и вообще сколько хотите. Но использование одноточечных множеств — простейший вариант. Лектор не хотел обременять слушателей дополнительным рассуждением, без которого можно обойтись.

А вот использовать бесконечные множества $F_k$ не удастся. Постройка развалится (фактически придётся сослаться на несчётность отрезка, которую придётся доказать другим способом, но тогда не стоит городить огород с теоремой Бэра).

cxzbsdhwert в сообщении #1713598 писал(а):

Ну хорошо, Вы же согласитесь, что если я на второй импликации в качестве следствия положу неодноточечное множество, то такого противоречия не произойдёт?

И фиг с ним. Ваша постройка развалилась, потому что Вы взяли неудачный блок. Хотя, если это множество конечное, то нужно взять ещё маленький кирпичик и в нужное место его воткнуть, чтобы укрепить всё сооружение. Я выше упоминал, что это за "кирпичик".

cxzbsdhwert в сообщении #1713616 писал(а):

tolstopuz в сообщении #1713613 писал(а):

Выбирается та тропка, которая ведет к желаемому результату, в данном случае верному доказательству.

Тогда истинность зависит от желания, а это не так.

Истинность не зависит от желания. От желания зависит способ доказательства.

cxzbsdhwert в сообщении #1713616 писал(а):

Да, наверное у причины может быть много следствий. Тогда наверное причина истинна если истинны все следствия. Или может у каждой причины есть ложные следствия и не в этом дело? Не знаю, я уже запутался

Это ерунда. Математическая логика устроена так, что из истинных утверждений следуют только истинные. Если Вы исходили из истинных утверждений и нигде не наврали в своих рассуждениях, то результат будет истинным. Но Вы так путаетесь в самых простых рассуждениях, что за ваши выводы я не поручусь.

[cxzbsdhwert]

Mikhail_K, skobar

Дискуссия сводится к спору о содержании теоремы.

Допустим теорема строго формулируется так: для любого замкнутого множества $F$ и любого нбчс набора замкнутых множеств $F_n$, объединение которых равно $F$ существует пересекающийся с $F$ интервал и найдётся множество из набора $F_n$ такое что пересечение лежит в нём.
Тогда противоречие возникает, поскольку любой набор, в частности, одноточечный должен по Теореме иметь $F_n$ содержащий пересечение интервала, и в тоже время пересечение любого интервала с отрезком имеет более одной точки.

Но, если строгая формулировка теоремы начинается иначе: для любого замкнутого множества $F_n$ найдётся нбчс набор ... такой что ...
Тогда мы не в праве утверждать о противоречии в случае с одноточечным набором, потому что теорема не утверждает что это тот набор для которого существует $F_n$ в котором лежит пересечение, поскольку теорема, ещё раз, не утверждает, что это верно для всякого набора. Она утверждает для всякого $F$, но не для всякого нбчс набора, объединение которого равно $F_n$

Вы согласны с тем, что если содержание теоремы таково (пусть даже не таково, но если было бы таковым), то ограничение рассмотрением только одноточечного случая к противоречию с предположением о нбчс отрезка не приводит?

[skobar]

cxzbsdhwert
Похоже, что удалось выявить, в чем именно у вас проблема с пониманием :)

cxzbsdhwert в сообщении #1713675 писал(а):

Допустим теорема строго формулируется так: для любого замкнутого множества $F$ и любого нбчс набора замкнутых множеств $F_n$, объединение которых равно $F$ существует пересекающийся с $F$ интервал и найдётся множество из набора $F_n$ такое что пересечение лежит в нём.

Это абсолютно верная формулировка теоремы.

cxzbsdhwert в сообщении #1713675 писал(а):

Но, если строгая формулировка теоремы начинается иначе: для любого замкнутого множества $F_n$ найдётся нбчс набор ... такой что ..

Видимо, вы все же имели ввиду здесь $F$, не $F_n$. В любом случае вот это неправильная формулировка теоремы. У меня и было подозрение, что вы трактуете её именно так, отсюда возник вопрос к вам выше. Надеюсь, он сработал и правильное понимание теоремы достигнуто :)

[cxzbsdhwert]

tolstopuz в сообщении #1713582 писал(а):

cxzbsdhwert в сообщении #1713580 писал(а):

не всякое счетное объединение замкнуто?

Конечно. Поэтому отдельно требуется доказательство того, что отрезок замкнут.

Нет, всё-таки вне зависимости от формулировки теоремы тут ошибка в рассуждениях.

Для того чтобы вообще перейти к применению теоремы Бэра нужно не только доказать что нбчс отрезок замкнут, но и нужно доказать что объединение именно счетного набора одноточечных множеств его элементов замкнуто.
Только после этого мы сможем утверждать что оно (объединение) ему равно, и только после этого, как и спрашивал @skobar, будут все "входные" для того что применять теорему Бэра и показывать противоречия с интервалами.

Может ли быть замкнутым в $\mathbb R$ объединение именно счетного набора замкнутых в $\mathbb R$ непересекающихся множеств, если такое объединение ещё и ограничено?

Даже если Вы ответите что мы можем полагать объединение замкнутым потому полагаем его равным нбчс отрезку, который точно замкнут, то это всё равно означает, что на том шаге на котором Вы такое предположение сделаете немедленно возникает противоречие с вышенаписанным (если оно верно), и до Теоремы Бэра Вы просто не успеете дойти.

-- 30.12.2025, 11:34 --

skobar в сообщении #1713679 писал(а):

А вот это не правильная формулировка теоремы

Да пожалуйста. Вот только есть один вопрос: а каковы доказательства того что эта формулировка неправильная?

[Someone]

cxzbsdhwert в сообщении #1713680 писал(а):

Для того чтобы вообще перейти к применению теоремы Бэра нужно не только доказать что нбчс отрезок замкнут, но и нужно доказать что объединение именно счетного набора одноточечных множеств его элементов замкнуто.

Вы продолжаете писать глупости несмотря на то, что Вам уже объясняли:
1) замкнутость отрезка доказывается прямо по определению замкнутого множества и не использует ничего, кроме этого определения; в частности, мощность отрезка не играет при этом никакой роли;
2) объединение всех одноточечных подмножеств отрезка равно самому этому отрезку и потому замкнуто, и не требуется это доказывать отдельно;

По моему мнению, мы имеем дело с троллингом.

[cxzbsdhwert]

Someone
Я с уважением отношусь ко времени которое люди тут потратили.
Ваш комментарий предусмотрел:

Цитата:

Даже если Вы ответите что мы можем полагать объединение замкнутым потому полагаем его равным нбчс отрезку, который точно замкнут, то это всё равно означает, что на том шаге на котором Вы такое предположение сделаете немедленно возникает противоречие с вышенаписанным (если оно верно), и до Теоремы Бэра Вы просто не успеете дойти.

[Someone]

cxzbsdhwert в сообщении #1713685 писал(а):

Даже если Вы ответите что мы можем полагать объединение замкнутым потому полагаем его равным нбчс отрезку

Это глупость. Объединение всех одноточечных подмножеств отрезка равно отрезку потому, что оно содержит все точки отрезка и не содержит лишних точек. А вовсе не потому, что мы "полагаем его замкнутым".

В общем, предположение о троллинге остаётся в силе.

[cxzbsdhwert]

Someone в сообщении #1713687 писал(а):

cxzbsdhwert в сообщении #1713685 писал(а):

Даже если Вы ответите что мы можем полагать объединение замкнутым потому полагаем его равным нбчс отрезку

Это глупость. Объединение всех одноточечных подмножеств отрезка равно отрезку потому, что оно содержит все точки отрезка и не содержит лишних точек. А вовсе не потому, что мы "полагаем его замкнутым".

В общем, предположение о троллинге остаётся в силе.

Вы возможно не внимательно прочитали сообщение.

Написано не о равенстве объединения а о его замкнутости. Вы написали что оно замкнуто потому что оно равно замкнутому по определению отрезку.

Я Вам показываю, что в тоже время верно(верно же?) утверждение о том что не может быть замкнутым в $\mathbb R$ объединение именно счетного набора замкнутых (по крайней мере замкнутых и не более чем счётных, в частности конечных) в $\mathbb R$ непересекающихся множеств, если такое объединение ещё и ограничено.

То есть объединение замкнуто по предположению о том что оно равно замкнутому отрезку И не замкнуто по верхнему утверждению.

Противоречие.

[tolstopuz]

cxzbsdhwert в сообщении #1713688 писал(а):

Я Вам показываю, что в тоже время верно(верно же?) утверждение о том что не может быть замкнутым в $\mathbb R$ объединение именно счетного набора замкнутых в $\mathbb R$ непересекающихся множеств, если такое объединение ещё и ограничено.

Хотя это не имеет отношения к обсуждаемому доказательству, но если бы это было верно, вы могли бы создать новое доказательство несчетности отрезка, без теоремы Бэра. Это интересно, но ваше утверждение неверно: возьмите $F_1=\{0\}$, $F_n=\{\frac1{n-1}\}$ при $n\ge2$. Объединение замкнуто.

[cxzbsdhwert]

tolstopuz в сообщении #1713691 писал(а):

cxzbsdhwert в сообщении #1713688 писал(а):

Я Вам показываю, что в тоже время верно(верно же?) утверждение о том что не может быть замкнутым в $\mathbb R$ объединение именно счетного набора замкнутых в $\mathbb R$ непересекающихся множеств, если такое объединение ещё и ограничено.

Хотя это не имеет отношения к обсуждаемому доказательству, но если бы это было верно, вы могли бы создать новое доказательство несчетности отрезка, без теоремы Бэра. Это интересно, но ваше утверждение неверно: возьмите $F_1=\{0\}$, $F_n=\{\frac1{n-1}\}$ при $n\ge2$. Объединение замкнуто.

1. Возьмём "обратный" набор к тому, который Вы привели: $F_1=\{1\}, F_n=\{1-\frac1{n-1}\} \text{при } \space n\geq 2$.
2. Объединение такого набора тоже замкнуто.
3. По теореме, которую я ранее упоминал — конечное объединение замкнутых множеств замкнуто.
4. По другой не менее важной теореме — объединение не более чем счетного набора не более чем счётных множеств не более чем счетно.
5. Тогда объединение Вашего множества с предельной точкой $0$ с моим множеством с предельной точкой $1$ — замкнуто и не более чем счетно.

6. Поскольку $0$ и $1$ предельны но и граничны, пересечение любого интервала с таким объединённым множеством состоит из более чем одной точки (ну или пусто, если не пересекаются).
7. Дальше происходит противоречие с Теоремой Бэра, поскольку будучи замкнутым и не более чем счетным оно равно объединению нбчс набора одноточечных множеств в одном из которых должно лежать пересечение хоть какого-нибудь интервала. А пересечение интервала всегда больше чем из одной точки для данного множества.

[Mikhail_K]

cxzbsdhwert в сообщении #1713698 писал(а):

6. Поскольку $0$ и $1$ предельны но и граничны, пересечение любого интервала с таким объединённым множеством состоит из более чем одной точки (ну или пусто, если не пересекаются).

Это неверно. Пересечение интервала $(0.49,0.51)$ с таким объединённым множеством состоит из одной точки $0.5$.