А что это?
Берем кольцо

. Фиксируем
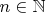
. Рассмотрим отношение

на

:

. Отношение эквивалентности оказывается согласованным с операциями на

(такие отношения называют конгруэнциями), значит оно порождает факторструктуру, которая в данном случае оказывается коммутативным ассоциативным кольцом с единицей и называется
кольцом вычетов по модулю 
. Как множество оно конечное (состоит из

элементов). Классы называются
вычетами по модулю 
и обычно обозначаются
![$[0]_n, ... , [n-1]_n$ $[0]_n, ... , [n-1]_n$](https://dxdy-01.korotkov.co.uk/f/c/1/8/c187f512dd6753bedda82c506115640882.png)
. Если у нас

,то

- это на самом деле
![$[8]_3 = [2]_3$ $[8]_3 = [2]_3$](https://dxdy-03.korotkov.co.uk/f/2/9/f/29f89d6756cc621ceda7d3357dd4e0fd82.png)
и как множество оно бесконечное (состоит из всех целых чисел, которые дают остаток

при делении на

)
В виду теоремы о согласованности операций, на письме можно опускать обозначения классов и вместо них писать голые целые числа. Вместе с этим можно взаимозаменять операции

и

друг с другом. Именно поэтому, например, законны записи вида

. По-хорошему, это надо писать следующим образом:
![$[8]_3 +_{\mathbb Z \slash 3 \mathbb Z} [1]_3 = [8 +_\mathbb Z 1]_3 = [9]_3 = [0]_3$ $[8]_3 +_{\mathbb Z \slash 3 \mathbb Z} [1]_3 = [8 +_\mathbb Z 1]_3 = [9]_3 = [0]_3$](https://dxdy-04.korotkov.co.uk/f/3/4/4/34487027c10d5f8155125394ead3a3c082.png)
ну или по крайней мере

. Но так как с операциями все согласовано, и отношения

и

оба удовлетворяют условиям рефлексивности, симметричности и транзитивности, значит можно делать "отождествления" на письме. Но, имхо, это все конкретные теоремы, которые надо доказывать.