Элементарная алгебра для отстающих

[horda2501]

Меня сбивает с толку вот что. Видимо, я здесь не допонимаю и вообще не правильно представляю. Я получаю эту точку на абсциссе (с координатой 0) когда подставляю 0 в качестве значения $x$ из знаменателя. То есть, как получить обнуление значения этих дробей? Один из множителей равен 0. Как в числителе, так и в знаменателе. До сих пор это всегда работало. Но когда в знаменателе, например, $x(x-1)$, это я ещё смирялась, а когда уже стало просто $x$, то не смогла

[provincialka]

horda2501, а вы все-таки скажите, каков смысл метода интервалов? Пока он у вас напоминает какие-то магические действия...

[Mihr]

horda2501 в сообщении #1695366 писал(а):

Я получаю эту точку на абсциссе (с координатой 0) когда подставляю 0 в качестве значения $x$ из знаменателя. То есть, как получить обнуление значения этих дробей?

Вы очень непривычно изъясняетесь. Трудно понять, о чём Вы вообще спрашиваете. Попробуйте более строгим языком изложить свои затруднения.

horda2501 в сообщении #1695366 писал(а):

например, $x(x-1)$, это я ещё смирялась, а когда уже стало просто $x$, то не смогла

Может, Вам легче будет смириться, если заметить что $x-0=x$?

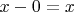
Ещё раз: если в числителе либо в знаменателе встречается сомножитель вида $x-a$, то в точке $a$ значение дроби меняет знак (с плюса на минус, либо, наоборот, с минуса на плюс). То что разность $x-a$ может быть в знаменателе, и в точке $a$ в этом случае знаменатель обращается в ноль, неважно. Вас ведь никто не просит вычислить значение дроби в точке $a$. Здесь важно лишь то, что если $x<a$, то разность $x-a$ имеет один знак, а если $x>a$, то другой. (В первом случае минус, во втором - плюс). Только это и использует метод интервалов.