Я правильно нахожу первый член этой прогрессии, если
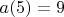
, а
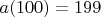
? Разность членов поделить на количество шагов.
Худший способ изучать математику - это запоминать "заклинания" вида: "Если взять разность старшего и младшего членов арифметической прогрессии и поделить на количество шагов, то получится ...."
В математике нужно запоминать
только обозначения. Но это язык такой, без запоминания никак нельзя.
Про всё остальное нужно
знать и понимать - откуда оно берется.
Тогда и ошибиться будет сложнее, и проверить себя \ найти ошибку не составит труда.
"Общий случай" (не совсем общий, но да ладно

) данной задаче заключается в следующем:
1. Записать два члена арифметической последовательности, через первый член

и разность ("величину шага")

. Это уже Вам подсказали выше:

и
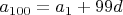
.
2. Приравнять получившиеся выражения для

и

значениям, которые заданы для них в условиях.
Получится два уравнения для двух неизвестных.
3. Решить получившуюся систему из двух уравнений любым способом, который Вы знаете.
В процессе решения, кстати, в числе прочих результатов и получится правило в правильной формулировке:
"Если взять разность старшего и младшего членов арифметической прогрессии и поделить на количество шагов, то получится ...."
-- 13.09.2025, 20:03 --А действительно общий случай - это не считать номера членов последовательности заданными, а обозначить из буквами:
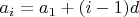
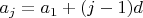
Теперь, считая
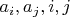
известными, нужно решить систему уравнений относительно неизвестных

и
