Элементарная алгебра для отстающих

[wrest]

horda2501 в сообщении #1701130 писал(а):

Используя ХСАП, найдите первый член и разность АП, если $4a+12a=9$ и $9a \cdot 7a=12$.

проверьте нет ли ошибки в условиях, задача не похожа на школьную

[EUgeneUS]

wrest в сообщении #1701214 писал(а):

проверьте нет ли ошибки в условиях, задача не похожа на школьную

Это просто некорректная запись. Выше же разобрались.
ТС сразу сказала, что не знает, как нижние индексы ставить. Ей показали.

[wrest]

EUgeneUS в сообщении #1701215 писал(а):

Это просто некорректная запись. Выше же разобрались.
ТС сразу сказала, что не знает, как нижние индексы ставить. Ей показали.

Это я учёл, но задача продолжает оставаться непохожей на школьную.
Попррбуйте решить в "корректной" записи

Booker48 в сообщении #1701133 писал(а):

$a_4+a_{12}=9$ и $a_9 \cdot a_7=12$

и увидете :)

[EUgeneUS]

wrest в сообщении #1701217 писал(а):

и увидете :)

Всё получилось.
Да, выражения довольно громоздкие, но никаких комплексных корней не вылезло.

-- 10.09.2025, 09:13 --

Еще нужно быть аккуратноисо знаками: там два решения, отличающиеся знаками у радикалов.

[wrest]

EUgeneUS в сообщении #1701218 писал(а):

Да, выражения довольно громоздкие, но никаких комплексных корней не вылезло.

И решений два.
Ну и -- вам удалось использовать "Характеристическое свойство арифметической прогрессии" при решении?
С учетом хода решения и полученного вами ответа -- задача похожа на школьную задачу по теме арифметических прогрессий?

[EUgeneUS]

wrest в сообщении #1701219 писал(а):

Ну и -- вам удалось использовать "Характеристическое свойство арифметической прогрессии" при решении?

Пришлось погуглить - что это такое
Нет, не использовал.

wrest в сообщении #1701219 писал(а):

С учетом хода решения и полученного вами ответа -- задача похожа на школьную задачу по теме арифметических прогрессий?

Вполне.

-- 10.09.2025, 09:25 --

EUgeneUS в сообщении #1701220 писал(а):

Нет, не использовал.

Если есть желание, то можно использовать для упрощения первого уравнения

-- 10.09.2025, 09:27 --

Тогда и со вторым можно удобную штуку сделать

[wrest]

EUgeneUS в сообщении #1701220 писал(а):

Нет, не использовал.

Из первого равенства $a_4+a_{12}=9$, по ХСАП, немедленно следует, что $a_8=4,5$ (подставьте оба полученных вами решения и убедитесь, что в обоих $a_8=4,5$).

Вероятно, во втором равенстве ошибка в переписывании условий.
Ну да ладно, придёт ТС -- пусть в задачник заглянет ещё раз.

[EUgeneUS]

wrest в сообщении #1701221 писал(а):

тогда первое равенство $a_4+a_{12}=9$ делает систему несовместной т.к. из него, по ХСАП, немедленно следует, что $a_8=4,5$.

С чего бы оно делает систему несовместной?

[wrest]

EUgeneUS в сообщении #1701222 писал(а):

С чего бы оно делает систему несовместной?

Ну когда вы замените $a_i$ на их выражения через $a_1$, $i$ и $d$, у вас получится несовместная система если второе равенство записать как $a_7+a_9=12$ а не как $a_7 \cdot a_9 =12$
Я просто пытаюсь угадать где ошибка в условиях, исправление которой сделает задачу решаемой в уме, при том с использованием ХСАП, как и положено школьным задачам.

[EUgeneUS]

А почему задача должна решаться в уме?

[wrest]

horda2501 в сообщении #1701130 писал(а):

Как видите, не смогла найти как обозначить члены прогрессии в виде буквы и номера внизу справа. Как это сделать?

Если не умеете писать нижний индекс, можете писать его в скобках, например $a(4)+a(12)=9$

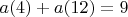-- 10.09.2025, 10:00 --

EUgeneUS в сообщении #1701224 писал(а):

А почему задача должна решаться в уме?

Ну это предположение. Задача школьная, тема простая. Значит, у нас с вами такая задача решается обычно в уме. Ну а школьнику надо подробно писать, конечно. Чтобы когда он(а) закончит школьную программу, и возможно пару семестров матана-линала, такие задачи у него(неё) тоже решались бы в уме. Как-то так...

-- 10.09.2025, 10:18 --

EUgeneUS в сообщении #1701220 писал(а):

Пришлось погуглить - что это такое

Кстати. Ну вот вы нагуглили что ХСАП-ом оказывается называют свойство
$a_n=\dfrac{a_{n-1}+a_{n+1}}{2}, n>1$
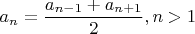
Вы же, наверное, сразу и обобщили это (в уме) до очевидного $a_n=\dfrac{a_{n-k}+a_{n+k}}{2}, n>k$
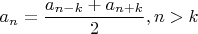
Тяга к обобщениям это ведь тоже результат обучения. У школьников такого видения обычно нет, особенно у "отстающих", как заявлено в названии темы.

[Booker48]

Сорри, давая свой совет, я не обратил внимание на необходимость использования ХСАП.
Тогда, имхо, и впрямь можно в уме решить. )))
Если переписать второе уравнение как $(a_8+d)(a_8-d)=12$.

[wrest]

Booker48 в сообщении #1701229 писал(а):

Если переписать второе уравнение как $(a_8+d)(a_8-d)=12$.

Конечно, получается квадратное уравнение с двумя решениями $\pm\sqrt{4,5^2-12}=\pm\dfrac{\sqrt{33}}{4}$ что меня и смутило, т.к. в школьной задаче вылезает вот такой квадратный корень. И это если ТС умножит на 4, а так-то $\pm\sqrt{8,25}$ - ну очень странно..., и два решения.