В примере в учебнике была функция

и там волна просто сжималась от плюс-минус

до

в зависимости от конца. То есть, делался "шаг" по числовой прямой (если справа на налево)
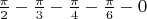
. Числовой коэффициент

значит два шага и ты попадаешь в

.
Про то, что коэффициент

значит два шага по какой-то шкале, Вы придумали. Это совершенно не так.
Из

мы действительно попадаем в точку

, а из

куда? По Вашей шкале получилось бы, что из точки

мы попадаем в

, а на самом деле в

. И тогда при подставлении

вместо

в функцию

получится

. То есть в точке

функция

принимает то же значение, что и функция

в точке

. С другими точками всё работает так же; это и значит, что к графику функции

мы переходим от графика обычного косинуса сжатием в два раза вдоль оси

.
Сжатие в два раза - это деление на два, и работает оно именно так.
Возможно, лучше попробовать понять алгебраически. Только с функцией

. Затруднение вот в чём. С растяжением ясно. Мол, от точки пересечения графика с осью абсцисс (то есть,

) нужно сместить эту точку в

. Но не является понятным действие сжатия в таком случае. Есть та же точка пересечения

. Есть, например, банальный коэффициент сжатия

. Куда я должна сжать? Если

разделить на

, то это точка

, а если на

, то

. Но точка

ближе к исходному

, а должна быть дальше, ведь коэффициент сжатия больше. Где ошибка в понимании?