3#: n=1: 4=1
5#: n=7: 2=2, 4=3, 6=2
7#: n=47: 2=14, 4=15, 6=14, 8=2, 10=2
11#: n=479: 2=134, 4=135, 6=142, 8=28, 10=30, 12=8, 14=2
13#: n=5759: 2=1484, 4=1485, 6=1690, 8=394, 10=438, 12=188, 14=58, 16=12, 18=8, 22=2
17#: n=92159: 2=22274, 4=22275, 6=26630, 8=6812, 10=7734, 12=4096, 14=1406, 16=432, 18=376, 20=24, 22=78, 24=20, 26=2
19#: n=1658879: 2=378674, 4=378675, 6=470630, 8=128810, 10=148530, 12=90124, 14=33206, 16=12372, 18=12424, 20=1440, 22=2622, 24=1136, 26=142, 28=72, 30=20, 34=2
23#: n=36495359: 2=7952174, 4=7952175, 6=10169950, 8=2918020, 10=3401790, 12=2255792, 14=871318, 16=362376, 18=396872, 20=61560, 22=88614, 24=48868, 26=7682, 28=5664, 30=2164, 32=72, 34=198, 36=56, 38=2, 40=12

 и
и  .
. больше
больше  , т.е. не
, т.е. не  и
и  , вот и получается разница в
, вот и получается разница в  .
.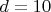
 ???
??? и
и  . Плохо искали видимо ...
. Плохо искали видимо ... и
и  . Доказана оценка:
. Доказана оценка:  Для распределения сумм функций простых чисел представляет интерес оценка модуля разности
Для распределения сумм функций простых чисел представляет интерес оценка модуля разности  и
и  . Выражение (5) соответствует оценке:
. Выражение (5) соответствует оценке:  Известна эквивалентная формулировка гипотезы Римана:
Известна эквивалентная формулировка гипотезы Римана: Эквивалентной формулировке гипотезы Римана (7) соответствует оценка:
Эквивалентной формулировке гипотезы Римана (7) соответствует оценка: 
 . Мало ли кто как именно что считает, кто-то с нуля, кто-то с единицы, плюс поведение на границах могут учитывать по разному.
. Мало ли кто как именно что считает, кто-то с нуля, кто-то с единицы, плюс поведение на границах могут учитывать по разному.
 раз дольше.
раз дольше. чисел и для каждого посчитать gcd()?! Даже после хорошей оптимизации, на которую уйдёт не один день, скорость явно не превысит
чисел и для каждого посчитать gcd()?! Даже после хорошей оптимизации, на которую уйдёт не один день, скорость явно не превысит  в секунду, а значит
в секунду, а значит  секунд на всё или более 190 лет. Про 59# с его полумиллионом лет лучше вообще молчать.
секунд на всё или более 190 лет. Про 59# с его полумиллионом лет лучше вообще молчать. занял порядка 7ч или
занял порядка 7ч или  в секунду. Всего втрое быстрее оценки. Но 60 лет вместо 190 всё равно никак не радуют.
в секунду. Всего втрое быстрее оценки. Но 60 лет вместо 190 всё равно никак не радуют.