3#: n=1: 4=1
5#: n=7: 2=2, 4=3, 6=2
7#: n=47: 2=14, 4=15, 6=14, 8=2, 10=2
11#: n=479: 2=134, 4=135, 6=142, 8=28, 10=30, 12=8, 14=2
13#: n=5759: 2=1484, 4=1485, 6=1690, 8=394, 10=438, 12=188, 14=58, 16=12, 18=8, 22=2
17#: n=92159: 2=22274, 4=22275, 6=26630, 8=6812, 10=7734, 12=4096, 14=1406, 16=432, 18=376, 20=24, 22=78, 24=20, 26=2
19#: n=1658879: 2=378674, 4=378675, 6=470630, 8=128810, 10=148530, 12=90124, 14=33206, 16=12372, 18=12424, 20=1440, 22=2622, 24=1136, 26=142, 28=72, 30=20, 34=2
23#: n=36495359: 2=7952174, 4=7952175, 6=10169950, 8=2918020, 10=3401790, 12=2255792, 14=871318, 16=362376, 18=396872, 20=61560, 22=88614, 24=48868, 26=7682, 28=5664, 30=2164, 32=72, 34=198, 36=56, 38=2, 40=12
29#: 2=214708724 4=214708725 6=280323050 8=83120450 10=97648950 12=68713708 14=27403082 16=12199404 18=14123368 20=2594160 22=3324402 24=2100872 26=386554 28=324792 30=154220 32=10128 34=15942 36=7228 38=570 40=1464 42=272 44=12 46=2
31#: 2=6226553024 4=6226553025 6=8278462850 8=2524575200 10=2985436650 12=2206209208 14=903350042 16=423955224 18=512670088 20=106604280 22=126682650 24=88337252 26=18298102 28=16461600 30=9169532 32=833688 34=1075458 36=620632 38=77042 40=128988 42=40636 44=3516 46=1794 48=1296 50=504 52=20 54=84 56=12 58=2

 .
. до
до  , где как Вы знаете, взаимно простые все простые. Конечно, "дикая идея", но все же было интересно.
, где как Вы знаете, взаимно простые все простые. Конечно, "дикая идея", но все же было интересно.  не превосходят
не превосходят  , может это как-то поможет, особенно если брать
, может это как-то поможет, особенно если брать  , когда относительная флуктуация
, когда относительная флуктуация  будет бесконечно малой ...
будет бесконечно малой ... ? Я когда-то давно пытался "вручную" проверять (до
? Я когда-то давно пытался "вручную" проверять (до  ) и были погрешности, но небольшие, если память не подводит, типа
) и были погрешности, но небольшие, если память не подводит, типа  .
. связана с тем что в программе нигде не проверяется равенство чего-либо числителю, лишь на взаимную простоту с
связана с тем что в программе нигде не проверяется равенство чего-либо числителю, лишь на взаимную простоту с  , и среди всего множества значений
, и среди всего множества значений  ни одно из этих количеств разумеется
ни одно из этих количеств разумеется  равно не будет.
равно не будет. существуют определенные формулы.
существуют определенные формулы.





 не сокращать, то деление будет на степени двойки, в остальном вроде похоже на ваше:
не сокращать, то деление будет на степени двойки, в остальном вроде похоже на ваше: имеет место неравенство:
имеет место неравенство: причем
причем  зависят от
зависят от  . Доказательство не в одну строчку.
. Доказательство не в одну строчку. , то получим теорему Чебышева:
, то получим теорему Чебышева:
 и получаем асимптотический закон распределения простых чисел:
и получаем асимптотический закон распределения простых чисел:
















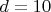
 ???
??? и
и  .
.