задача.доказать , что множество попарно не пересекающихся букв

на плоскости не более чем счетно.

Взял решение из ульянова,вроде разобрался,но есть вопрос-когда проверяется пересечение треугольника с другими буквами Т,почему именно такое?
Например если я расположу букву

под неким углом,то пересечение будет совершенно другим
Сейчас выложу свое решение
Задача не раз уже обсуждалась.
0)Достроим букву

до треугольника
1)На букве

определяем точки ABCD
2)в треугольнике
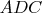
берем произвольную точку

с рац координатами
3)в треугольнике

берем точку

с рац координатами
4)точка

лежит в вертикальном угле

где

-это середина

(это шапка буквы

.

-ножка)
5)Каждая сторона треугольника

пересекает линию треуг

1 раз. и точка

находится внутри этого треугольника
6)[а вот тут возникает вопрос]
Предполагаем,что для

состоящей из отр

и

получилась та же тройка чисел

. Тогда

лежит в 1 из 3ех частей
a)

-лежит со стороны

-выходящий из нее отрезок не может пересечь

и не пересечь



и

пересекутся
b)

лежит в
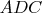

выходящий отрезок пересекает


должен пересечь AD DC
c)

лежит в

,

выходящий отрезок пересекает


пересечет и

и

Тогда разным буквам соотв-ют разные

7) Т.К каждой букве

ставится в соответ-ие эта тройка чисел

множество не пересекающихся букв

счетно.(т.к множество этих троек счетно)
-- 11.01.2015, 21:09 --Поясните пожалуйста 6 пункт.
Так как если я ориентирую вторую букву под углом,то будут совсем иные пересечения,но суть должна остаться та же
Просто,я уже не помню,что конкретно не понравилось преподавателю