В начале июля на блоге Тао
http://terrytao.wordpress.com/2007/03/18/why-global-regularity-for-navier-stokes-is-hard/ появилось несколько комментариев, которые мне кажутся интересными
2 July, 2014 at 12:36 pm anonymous писал(а):
I have searched all over the internet looking for the proof that having enstrophy bounded implies regularity for NS and/or Euler. The closest I can find is the Beale-Kato-Majda (BKM) vorticity blowup criteria (actually mentioned in the Clay problem statement). This is a time integral of the sup of the vorticity at each time slice — not enstrophy (space integral of vorticty squared). Maybe this blog has redefined enstrophy.
3 July, 2014 at 5:20 am Gandhi Viswanathan писал(а):
I believe Leray himself proved that the
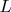
2 enstrophy remains bounded for regular solutions of the 3-D NS system. But for the 3-D Euler system, the enstrophy can remain bounded at the time of first breakdown. Here is an intro about the Euler eqs.: DOI: 10.1016/j.physd.2007.10.014
3 July, 2014 at 5:44 am Gandhi Viswanathan писал(а):
Going back to Leray, I think he focussed on L^p norms, whereas the enstrophy is an inhomogeneous Sobolev norm. But the key point is that, unlike kinetic energy, the enstrophy is subcritical for the 3-D NS system, so as long as the enstrophy remains bounded, singularities cannot form. The Euler eqs., in contrast, have a 2-parameter scale invariance, so we cannot use concepts like subcritical and supercritical in the same sense as for the NS eqs.
3 July, 2014 at 7:33 am anonymous писал(а):
I hope this clears it up.
“Similar to the situation with the energy-dissipation rate per unit mass ε(t), time averages of the enstrophy over arbitrary nonzero intervals are finite for weak solutions, but we would need to know more to confirm that solutions are regular over the interval [e.g., that the variance of the enstrophy is finite. This observation highlights the importance of intermittency in Navier-Stokes dynamics (Frisch 1995, Vassilicos 2000). Intermittency refers to the phenomena of rare but large fluctuations usually associated with turbulence. If enstrophy fluctuations are bounded at the level of the time average of the second moment, then solutions are regular. ” — Doering (2009)
So, if I am reading this correctly, it is enough to have the mean enstrophy be bounded over a time interval for weak solutions. However, strong solutions required the variance of the enstrophy to be bounded.
3 July, 2014 at 7:06 am Terence Tao писал(а):
Sorry, I was a bit careless in my previous comment: bounded enstrophy is known to imply regularity for Navier-Stokes (as can be seen for instance from the Prodi-Serrin regularity condition and Sobolev embedding), but this is not known for Euler.
-- 06.07.2014, 02:28 --Да, был еще один отдельмый комментарий
5 July, 2014 at 11:03 am Choro Tukembaev писал(а):
For 3D Euler equations the answer see
T.D. Omurov, (2013), Navier-Stokes problem for Incompressible fluid with viscosity // Varia Informatica 2013. Ed. M. Milosz, PIPS Polish Lublin, pp.137-158.
Read pages 147-151. There assessed the proximity of solutions of the Euler and NS when the viscosity tends to zero.
Но про этот материал мы уже знаем (правда опубликованный тем же автором в другом месте)
Рискну предположить, что статья написана на кыргызском языке.

Что до ее содержания, то это один из образцов переливания из пустого в порожнее.