|
|
2) По ситуации в целом: я заметил тенденцию (общую, это не наезд ни на кого конкретного), что есть некое непонимание между физиками и математиками по части уровня развития математики, описывающей теоретическую физику; часто я слышу "математики не разрешают, но давайте сделаем вот так", или "давайте сделаем вот так, хотя математики не знают, почему так можно". Так вот: довольно часто знают :) Действительно, в теоретической физике есть куча проблем, про которые математика не знает, но про многие вещи, про которые физики говорят, что про них математика не знает, математика на самом деле знает. Предлагаю в дальнейшем отслеживать этот момент, во избежание Хаоса. Тут есть два момента: 1) Да, знают. Но те математики, которые уже давно и аспирантуру-то закончили :-) А не те, которые на втором курсе начинают с физикой знакомиться. И книжек, в которых написано, что именно там знают математики, днём с огнём не сыщешь, приходится долго и глубоко копать, с применением пыток :-) [Так что, и физики на втором курсе часто такой глубокой и сурьёзной математики не знают, и не слышали о ней. Или едва начали слышать, и начинается смешной спор, когда физики перед сверстниками-математиками щеголяют знакомством с более крутой математикой.] 2) Как я уже говорил, позволение математиков физике не очень-то критично. Так что, разрешают математики или не разрешают - зачастую иррелевантно. И это не такая уж проблема для теоретической физики. А проблемы теоретической физики часто имеют характер, вообще не относящийся к разрешениям математиков. А математики довольно часто смотрят на теорфизику сквозь зелёные очки, и ничего, кроме проблем разрешений математиков не видят. И, пожалуй, вот что: Фразы "математики не разрешают, но давайте сделаем вот так", или "давайте сделаем вот так, хотя математики не знают, почему так можно", очень часто относятся к строгости рассуждений, а не к способу вычислений. То есть, физики совершают некоторый "скачок" к итогу, который математики "не одобряе" именно в смысле неправильности способа получения, а не в смысле претензий к итогу per se. Впрочем, на эту тему было уже сказано неоднократно: (Чё-та многабукав нацитировалось...)
Некоторые математики никак не могут понять, что в физике есть еще и НАБЛЮДЕНИЕ. И для физика оно намного важнее и первичнее, чем логическая строгость ("не легкомыслие"). Математики делают логически точные утверждения ни о чем (существующем в природе). А физики --логически неточные "о чем" (т.е. существующем в природе). А так чтобы "о чем" и в то же время точные, еще никому пока не удавалось. И не удастся, видимо, никогда. Соответственно физику нужен специфический квазиматематический аппарат. Ни один математик такой аппарат создать не сможет. Просто потому, что чисто логически такой аппарат создать невозможно. Математики (чистые) нелогично мыслить не умеют. Кстати нелогично еще не значит неправильно -- (это - М.) ни одному математику недоступно:-) Вопрос же не только в аппарате, а и в путях ПРИХОДА к этому аппарату. Чтобы к другим аппаратам приходить уметь. В т.ч. еще не существующим. Собственно в ЭТОМ и состоит деятельность физика-теоретика: угадывать аппарат, описывающий то или иное физическое явление. А уж "приводить в порядок" этот аппарат (если он новый, что крайне редко) -- это совсем другая профессия. Никогда не научишься профессиии физика, если будешь логическим пуристом.
...
На счет того, что почему же физики не приходят к полному бреду. Есть принципиальная разница между физикой и математикой. В физике есть "Верховный Судья" который иной раз говорит: "ты где-то заврался" (а вот чтобы найти где, тут полезны и чисто математические знания, но не они одни). В математике такого судьи нет, математики просто ВЫНУЖДЕНЫ быть пуристами. У физиков этой проблемы нет, но есть другие проблемы, отсутствующие у математиков. Итого: разные науки. ...Математикам нечем проверить свой результат, кроме подглядывания в ответы в конце задачника. А для физиков это было бы реальными вычислениями, невзирая на то, что у них может и не быть формально точного смысла. Да, чреватыми ошибками. Но ошибки можно потом найти и вычистить (например, экспериментом), а потом научиться делать это же без ошибок. Я понимаю ваше нежелание смириться с этим, у меня тоже где-то что-то внутри восстаёт, но в то же время я знаком слишком со многими примерами, когда физический успех вычислений наступал гораздо раньше, чем их математическая формализация. Пускай мы не знаем формально точного смысла этих наших вычислений, нас воодушевляет то, что существует физически точный смысл, который не требуется изобретать математикам - он заложен в природе (некоторые говорят - богом), и то, что мы не знаем одного (и тупо пользуемся некоторыми правилами), ничуть не хуже, чем когда мы не знаем другого. Прежде чем чего-то там посчитать -- полезно подумать, а имеют ли хоть какой-то смысл ваши считания. Ну т.е. обладаете ли вы хоть минимальной математической культурой. ...В физике сначала считают, а потом по результатам уже смотрят, имеют ли хоть какой-то смысл эти считания. И если оказывается, что имеют, даже если по мнению математиков не имеют - значит, просто математики чего-то не доработали. Никаких претензий к математической культуре друг друга физики в таких ситуациях не выдвигают, а напротив, поздравляют с успехом. Тут как раз уже упомянутое не один раз отличие между математикой и физикой играет роль. Математики опираются только на логику рассуждений. Когда логика начинает хромать, для них это катастрофа. Физики опираются и на логику, и на эксперимент. Если логика хромает, но эксперимент не указывает на проблему в этом месте - логически смутное место игнорируют и идут дальше.
Да, мы знаем, что реальные физические зависимости не являются функциями на континууме, и что применять к ним операции дифференцирования и интегрирования логически не более осмысленно, чем к строчкам символов. Но они ведут себя как функции на континууме, в том числе, как будто у них есть производные и первообразные, которые можно померить/пощупать другими способами. (Простейший пример: вторая производная от положения равна силе, которую можно померять динамометром.) Таким образом, реальные физические зависимости - не изоморфны, конечно, но - каким-то образом мономорфны этим самым функциям на континууме. Этим мы и пользуемся.
По крайней мере, пока - мономорфны. Завтра может появиться экспериментальный факт, не укладывающийся в эту схему, тогда мы будем её ломать, и строить новую схему. Такой временный статус для физики нормален. Вообще в физике типична такая ситуация: ответ известен, надо найти из каких аксиом этот ответ можно вывести. Причем так, чтобы из тех же аксиом следовала и вся остальная куча ответов, что мы знаем. Изначально заданных аксиом нет, даже правил вывода изначальных нет. А понадобится - и логику изменим (хотя и не склонны так уж сразу ни с того ни с сего). Ну с какой бы такой радости Вселенная была обязана подчиняться какой-то там логике, выдуманной каким-то там Аристотелем на провинциальной планетке в заштатной галактике...
Да нет, не жалко. Просто хотелось, чтобы по плотности можно было восстановить общую массу. Можно. Если перестанем называть плотность функцией, и для новой фигни введём новые правила употребления значка 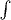 (который по-прежнему будем называть интегралом). Мне очень нравится вариант, когда плотность есть коцепь. Он очень хорошо ложится на физику.
|
|