Добрый день! Помогите пожалуйста с переводом такой теоремы:
Theorem (Mairhuber-Curtis)If
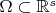
,
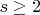
, contains an interior point, then there exist no Haar spaces of continuous functions except for one-dimensional ones.
Во-первых, я не встретил нигде на русском языке написания фамилий авторов, может есть какой-то устоявшийся вариант написания? Не знаю, верно ли будет написать Майрхубер-Кёртис? Ну и во-вторых как перевести "Haar spaces"? Сочетания "область Хаара" никогда раньше не слышал.
На всякий случай определение "Haar space":
Let the finite-dimensional linear function space
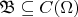
have basis
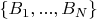
. Then

is a Haar space on

if
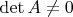
for any set of distinct

in

. Here A is the matrix with entries
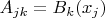
.
Моя попытка перевода:
Пусть
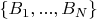
- базис конечномерного линейного функционального пространства
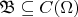
.

будет (областью Хаара?) на

, если
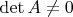
для множества попарно различных

. Здесь

- матрица с компонентами
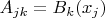
.
Заранее спасибо.



