равномерность

[Руст]

vicvolf в сообщении #631147 писал(а):

Руст в сообщении #628124 писал(а):

Продолжу

$$S_{gf}(A,B)=\sum_{A\le x\le B}g(f(i)),f(i)=\frac{1}{h_2}f_1(ih_1),A=\frac{a}{h_1},B=\frac{b}{h_1}.$$

Почему $f_1$?. Такой функции в условии нет.

Мы рассматриваем первоначально область, ограниченую кривой $a\le x\le b, 0\le y\le f_1(x)$. Далее наносим сетку целых точек $(ih_1,jh_2)$ и определяем функцию от целого аргумента, соответствующего этому разбиению $f(i)=\frac{1}{h_2}f_1(ih_1)$ и далее оперируем этой функцией при подсчете $g$ сумм.

[vicvolf]

В теме "Оценка нелинейных $g-$ сумм" Вы дали только лемму, которая позволяет определить влияние нелинейности на $g$ сумму в окрестности наклона $\alpha$ и оценку суммы в окрестности критической точки.
Разве тема закончена? Если нет, то желательно не обрывать тему посередине и закончить!

-- 15.10.2012, 11:42 --

Руст в сообщении #630437 писал(а):

На самом деле получаются более сильная равномерность распределения, чем необходимая для ГР и РГР равномерность в среднем.

А какая?

[Руст]

vicvolf в сообщении #631163 писал(а):

В теме "Оценка нелинейных $g-$ сумм" Вы дали только лемму, которая позволяет определить влияние нелинейности на $g$ сумму в окрестности наклона $\alpha$ и оценку суммы в окрестности критической точки.
Разве тема закончена? Если нет, то желательно не обрывать тему посередине и закончить!

-- 15.10.2012, 11:42 --

Руст в сообщении #630437 писал(а):

На самом деле получаются более сильная равномерность распределения, чем необходимая для ГР и РГР равномерность в среднем.

А какая?

Я вычислял $g-$ суммы в окрестности критической точки и сказал, что вычисления в окрестности точки с наклоном $\frac PQ$ сводятся (почти инвариантно) с помощью целочисленных дробно линейных преобразований с определителем $\pm 1$ к оценке суммы в окрестности критической суммы. Расширяя таким образом области около критической точки с постепенным добавлением областей с небольшим наклоном доходим до наклона 1. При этом на оцкнке $g$ суммы появится множитель $\ln R$ R- радиус кривизны, при сложении $\sum_{k=1}^{[\sqrt R]} \frac{\sqrt R}{k}$. Но это в общем случае при доказателстве равномерности дробных долей при отсутствии точек перегиба. При более точном оценивании в конкретных ситуациях степень логарифма можно снизить, так как коэффициенты перед каждом членом встречаются как отрицательные так и положительные. Но это более сложная оценка, которую я хочу провести.

[vicvolf]

Руст в сообщении #629827 писал(а):

Покажу, для чего надо исключить случай с точками перегиба. Пусть $f_1(x)=c(x-x_*)+d+O(|x-x_*|^\alpha ), \alpha>2.$ Это значит $x=x_*$ точка перегиба. Тогда в интервале $|x-x_*|<\beta h^{1/alpha}$ функция $f(y)=\frac{1}{h_2}f_1(yh_1)=f_2(y)+f_3(y),f_2(y)=cy+d, c=\frac{h_1}{h_2}f_1'(x_*),d=\frac{f_1(x)}{h_2}$ хорошо аппроксимируется линейной функцией, соответственно, когда $c=\frac{P}{Q}$ рационально (или хорошо приближается рациональным) числом (этого можно добиться за счет выбора $\frac{h_1}{h_2}$, сумма будет $S_{gf}(A,B)=O(R^{1-\frac{1}{\alpha}}),R=\frac{1}{h_1}$. Поэтому нельзя оценить лучше, чем $O(R^{2/3})$ как и у классиков, которые не выделяли в отдельный класс суммы с точкой перегиба. Соответственно, в случае наличия точек перегиба нет равномерности.

Функции $1/\ln^k x$ не имеют точек перегиба. Значит они обладают свойством равномерности в среднем?

[Руст]

vicvolf в сообщении #631192 писал(а):

Функции $1/\ln^k x$ не имеют точек перегиба. Значит они обладают свойством равномерности в среднем?

Я уже говорил, что сама плотность (как в случае простых $\frac{1}{\ln x}$ появляется уже после. Область для распределения простых эта область под гиперболой и не связано с логарифмом напрямую. Я уже говорид, что равномерность распределения простых по модулю 4, т.е. примерно одинаковое количество простых чисел видов $4kj\pm 1$ можно вывезти используя область круг. Для вашей задачи я вообще не знаю соответствия.

[vicvolf]

Руст в сообщении #630629 писал(а):

Сама плотность $\frac{1}{\ln x}$ вытекает совсем из других соображений, оно даже не связано (как я получаю) тем, что сумма $\sum_{k=1}^n \frac 1k$ или интегральный коэффициент $\int_1^n \frac{dx}{x}$ под гиперболой ведет себя как $\ln n$. Гипербола появляется из теории мультипликативных функций. Если мы имеем два ряда Дирихле
$\sum_k \frac{a_k}{k^s}, \sum_k \frac{b_k}{k^s}$, то произведению рядов соответствует ряд $\sum_n \frac{c_n}{n^s}, c_n=\sum_{kl=n}a_kb_l$, являющейся мультипликативной сверткой коэффициентов заданных рядов $a_k,b_k$. Соответственно сумма коэффициентов для 1 соответствует количеству целых точек под гиперболой. Вообще $\sum_{k=1}^n c_k = \sum_{ij\le n}a_ib_j$. Область суммирования состоит из $ij\le n$ целых точек под гиперболой. Вот откуда связь ГР с гиперболой.

Спасибо! Возникает только вопрос! Вы создаете теорию g-сумм, в том числе и нелинейных. Почему нельзя ее впрямую использовать для доказательста равномерности в среднем функции $1/\ln x$ от начала и до конца?

[Руст]

vicvolf в сообщении #631201 писал(а):

[
Спасибо! Возникает только вопрос! Вы создаете теорию g-сумм, в том числе и нелинейных. Почему нельзя ее впрямую использовать для доказательста равномерности в среднем функции $1/\ln x$ от начала и до конца?

Использовать то можно. Но что дает равномерность дробных долей $\frac{A}{\ln x}$, я не знаю.

[vicvolf]

Руст в сообщении #631203 писал(а):

Но что дает равномерность дробных долей $\frac{A}{\ln x}$, я не знаю.

Определение равномерности в среднем начинается с того, что существует такая функция и.т.д. Значит сначала надо доказать, что плотность распределения простых определяется функцией $\frac{1}{\ln x}$, а затем уже для определения количества простых через интеграл доказать равномерность этой функции в среднем с использованием g-сумм.

[Руст]

vicvolf в сообщении #631228 писал(а):

Руст в сообщении #631203 писал(а):

Но что дает равномерность дробных долей $\frac{A}{\ln x}$, я не знаю.

Определение равномерности в среднем начинается с того, что существует такая функция и.т.д. Значит сначала надо доказать, что плотность распределения простых определяется функцией $\frac{1}{\ln x}$, а затем уже для определения количества простых через интеграл доказать равномерность этой функции в среднем с использованием g-сумм.

Нет, в определении не конкретизируется вид функции плотности, необходимо только, чтобы она была гладкой в бесконечности. Конкретный вид с точностью до $O(x^{-\frac 12 +\epsilon})$ получается уже потом.

[vicvolf]

Руст в сообщении #630437 писал(а):

На самом деле получаются более сильная равномерность распределения, чем необходимая для ГР и РГР равномерность в среднем. Соответственно, они должны привести к решению задач, не вытекающих из ГР и РГР, например бинарная проблема Гольдбаха-Эйлера, бесконечность пар простых $(p,p+a)$ при любом четном $a$ (в частности решение проблемы близнецов, иницировавших эту тему), гипотеза Лежандра.

Хочу обратить внимание, что при решении проблемы бесконечности пар простых $(p,p+a)$ при любом четном $a$, начиная с a=6 при определении количества таких пар надо учесть, что данные пары имеют входящие кортежи. Напимер, для a=6 - кортежи (2,4) и (4,2). Поэтому плотность таких пар должна определяться с учетом этого. Я об этом писал в последнем сообщении своей темы "Об оценке количества некоторых групп чисел....".

-- 16.10.2012, 12:02 --

Руст в сообщении #631186 писал(а):

Но это более сложная оценка, которую я хочу провести.

Напишите, когда получите результат.

[vicvolf]

Руст в сообщении #631186 писал(а):

Я вычислял $g-$ суммы в окрестности критической точки и сказал, что вычисления в окрестности точки с наклоном $\frac PQ$ сводятся (почти инвариантно) с помощью целочисленных дробно линейных преобразований с определителем $\pm 1$ к оценке суммы в окрестности критической суммы. Расширяя таким образом области около критической точки с постепенным добавлением областей с небольшим наклоном доходим до наклона 1. При этом на оцкнке $g$ суммы появится множитель $\ln R$ R- радиус кривизны, при сложении $\sum_{k=1}^{[\sqrt R]} \frac{\sqrt R}{k}$. Но это в общем случае при доказателстве равномерности дробных долей при отсутствии точек перегиба. При более точном оценивании в конкретных ситуациях степень логарифма можно снизить, так как коэффициенты перед каждом членом встречаются как отрицательные так и положительные. Но это более сложная оценка, которую я хочу провести.

Не понял. Значит равномерность в среднем не выполняется в критических точках и на прямых с наклоном не превышающим 1? А на кривых с таким наклоном тоже не выполняется равномерность в среднем?

[Руст]

Дробные доли $\{f(n)\}$ для гладких функций не обладают свойством равномерности локально. Для них имеет место только равномерность в среднем если они не имеют точек перегиба. Но этого достаточно для многих задач.

[vicvolf]

Руст в сообщении #632435 писал(а):

Дробные доли $\{f(n)\}$ для гладких функций не обладают свойством равномерности локально. Для них имеет место только равномерность в среднем если они не имеют точек перегиба. Но этого достаточно для многих задач.

Значит Вы утверждается, что для всех гладких нелинейных функций, если они не имеют точек перегиба, имеется равномерность в среднем?

[Руст]

vicvolf в сообщении #632461 писал(а):

Руст в сообщении #632435 писал(а):

Дробные доли $\{f(n)\}$ для гладких функций не обладают свойством равномерности локально. Для них имеет место только равномерность в среднем если они не имеют точек перегиба. Но этого достаточно для многих задач.

Значит Вы утверждается, что для всех гладких нелинейных функций, если они не имеют точек перегиба, имеется равномерность в среднем?

Да.

[vicvolf]

Руст в сообщении #632580 писал(а):

vicvolf в сообщении #632461 писал(а):

Руст в сообщении #632435 писал(а):

Дробные доли $\{f(n)\}$ для гладких функций не обладают свойством равномерности локально. Для них имеет место только равномерность в среднем если они не имеют точек перегиба. Но этого достаточно для многих задач.

Значит Вы утверждается, что для всех гладких нелинейных функций, если они не имеют точек перегиба, имеется равномерность в среднем?

Да.

Почему задаю этот вопрос в разных вариантах, потому что:
1. После большого числа лемм напрашивается все таки теорема о том, что гдадкая нелинейная функция в отсутствии точек перегиба равномерна в среднем. Следствиями из нее может быть случай слабой равномерности для линейной функции и нелинейной функциями с точками перегиба.
2. С моей точки зрения, в начале работы желательно провести классификацию видов равномерности функций:
Если существует гладкая в бесконечности функция $f(x)$, что выполняется:

$$|\pi (f,a,b)- \int_a^b f(x)dx |<C(\epsilon)x^{k+\epsilon}$$

при любом $\epsilon >0$,
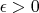
то f(x) при k>1/2 будет со слабой равномерностью,
при k=1/2 - со средней равномерностью,
при 0<k<1/2 - со слабой равномерность,
при k=0 - с абсолютной равномерностью.
Естественно, множество функций со слабой равномерностью включает в себя множество функций со средней равномерностью. Множество функций со средней равномерностью включает в себя множество функции с сильной равномеростью, а множество функции с сильной равномерностью включают в себя множество функций с абсолютной равномерностью.
Функции со слабой и средней равномерностью были указаны выше. Хотелось бы поговорить о множестве функций с сильной и абсолютной равномерностью. К функциям с абсолютной и соответственно с сильной равномерностью напрашивается отнести ступенчатую функцию, которая скачет на целое значение вверх и вниз при целых значениях х. Действительно площадь под этой функцией содержит только целые точки и других не содержит, поэтому ошибка не накапливается и равна 0. Конечно, в общем случае, данная функция не является гладкой и поэтому по определению равномерности не проходит. Но в частном случае функция y=b, где b - целое число и отрезок интегрирования целый, удолетворяет условию гладкости и так как ошибка в данном случае также равна 0, то подходит по определению к функциям с абсолютной, тем более сильной равномерностью, и тут возникает парадокс.
3. С точки зрения теории g-функций y=b, где b - целое число, является линейной функцией и поэтому должна быть отнесена к функциям со слабой сходимостью.