Оценим теперь

сумму около критической точки, пусть это будет минимум (максимум рассматривается аналогично), достигаемой в точке

. Пусть

. Оценим сумму

воспользовавшись этой леммой:


В дальнейшем будем пренебрегать изменением второй производной в небольших интервалах аппроксимации (около критической точки), точнее будем считать, что

Последнее условие выполняется при подсчете целых точек в области, ограниченной дважды непрерывно дифференцируемой границей, при любых шагах сетки
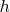
, меньших некоторого, за исключением окрестности точки перегиба, так как эквивалентен условию малости

. Тогда последним членом (с
![$]delta$ $]delta$](https://dxdy-01.korotkov.co.uk/f/0/9/a/09a8a1909daa71246b1a639d44f792be82.png)
) можно пренебречь несколько (незначительно) изменяя коэффициент перед предпоследним членом. Тогда

, а сумма с точностью до

вычисляется как площадь под параболой

Аналогично вычислим суммы между следующими уровнями функции

. Пусть

. Вычислим

сумму для этого случая поточнее (включая члены О(1)). Первые члены дадут

Обозначим для краткости записи обратную функцию через

в интервале суммирования. Тогда, если

, то и

и если

, то и

Аналогично для точки B. Таким образом:

где

Оценим теперь величины, обозначив

Тогда из квадратичного приближения вблизи

получаем:

Нам достаточно пользоваться приближениями, сохраняющими порядок величин. В этом смысле координата

, ближайшая сверху к точке

Средний наклон в интервале

и интервал суммирования между уровнями

. Отсюда получается, что до уровня

порядка

суммы

остаются ограниченными величиной порядка

, положительными в окрестности

и отрицательными, когда

. Более точно коэффициент можно вычислить сведя к знакопеременной сумме или интегралу. Сформулируем и докажем соответствующую лемму:
Лемма 5. Пусть

минимальное значение,

и

Тогда


Доказательство. Рассмотрим вначале начальный уровень. В этом интервале функция хорошо приближается квадратичной аппроксимацией

Соответственно количество целых х, для которых

равно

Беря разбиение шага

получаем ошибку аппроксимации интеграла порядка

.
Между собой компенсируются

и

. Соответственно

Аналогично:

Пока наклон мал можно аналогично считать интеграл до

. При этом несложно показать, что ошибка будет о(С) даже пользуясь плохими оценками. Нам достаточно оценка, что вся сумма

. Т.е. взяв

получаем:


Интегралы в интервале

будут величиной порядка

, что и доказывает лемму.
Для

суммы точные значения интегралов не удалось посчитать. Минимальное значение достигается при

примерно
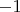
, максимальное значение при

, меньше 0.5. Можно и дальше суммировать. Только при этом надо считать так же

суммы для обратной функции.
Немного о том, для чего нужны оценки сумм около критической точки. Я уже говорил, что

суммы почти инвариантны относительно модулярных преобразований.

сумму в окрестности наклона

можно свести к

сумме в окрестности критической точки. Оценивая их и складывая можно уже получить оценку погрешности между количеством целых точек и площадью, у которой гладкая граница без точек перегиба, порядка

(у классиков степень

). Применяя оценки многократно индукцией оценку можно довести то показателя

, т.е. доказать равномерность в среднем распределения дробных долей

. Первоначально я использовал такой подход, потом захотел оценить точнее с учетом степеней от логарифмов. Но это более сложный и длинный путь, и я пожалуй здесь не буду приводить.
Покажу, для чего надо исключить случай с точками перегиба. Пусть

Это значит

точка перегиба. Тогда в интервале

функция

хорошо аппроксимируется линейной функцией, соответственно, когда

рационально (или хорошо приближается рациональным) числом (этого можно добиться за счет выбора

, сумма будет

. Поэтому нельзя оценить лучше, чем

как и у классиков, которые не выделяли в отдельный класс суммы с точкой перегиба. Соответственно, в случае наличия точек перегиба нет равномерности.