Господа, проверьте пожалуйста размышления.
Как придти к понятию гомотопии?
Гомотопия функций интуитивно понятна:
Пусть заданы функции

и

.
Итак, функции

и

назовем гомотопными, если существует гладкая гомотопия

.
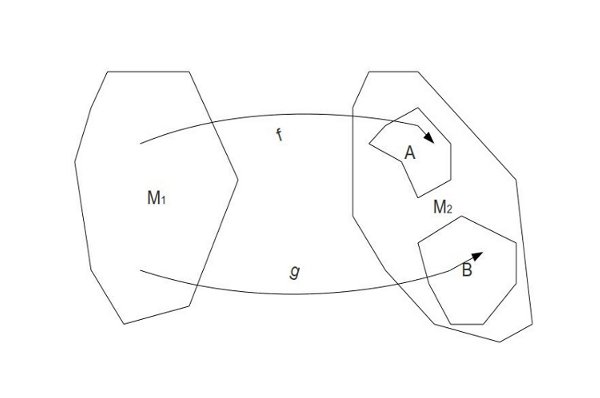
А вот множества

и

будут гомотопически эквивалентными. Иными словами, стягивая и растягивая эти множества можно из одного получить другое.
Теперь вопрос:
как обобщить понятие гомотопической эквивалентности без

и

?
Пусть заданы множества

и

и отображения

.
Вместо

и

можно взять само

( или

), вместо функции

берем тождественное преобразование а вместо функции

берем композицию

и возвращаемся к предидущему случаю. А именно:
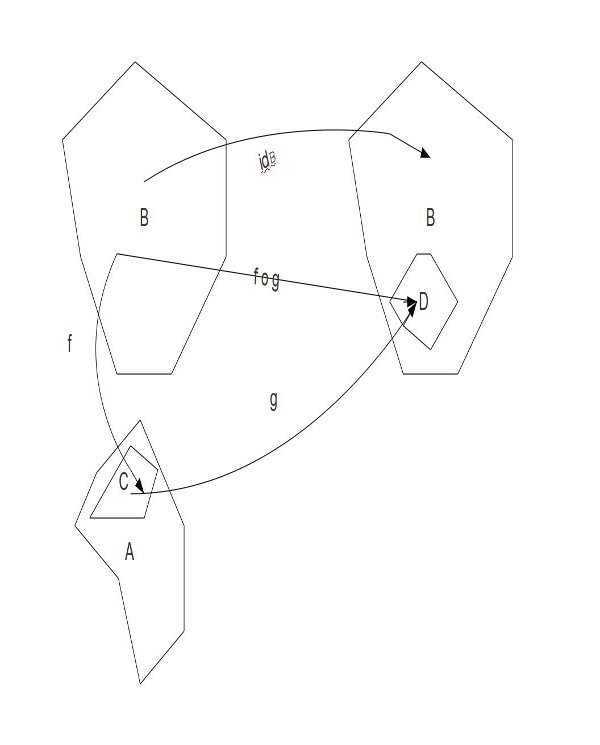
Отсюда понятно, что если можно подобрать такие

и

, чтобы

было гомотопо

, то

и

будут гомотопически эквивалентны.
А далшье все. Как отсюда и из соответствующей диграммы где

заменено на

понять, что они гомотопически эквивалентны, т.е. стягивая/растягивая одно можно получить другое?



