Ну и дискуссия разгорелась...
А слабо было начать с определения отношения порядка для десятичных дробей?
Я, например, не вижу ничего противоестественного в том, чтоба определить так:
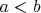
тогда и только тогда, когда старшая несовпадающая цифра у числа

меньше, чем у числа

.
По такому определению

, хотя это и противоречит тому, что
принято в арифметике действительных чисел. Аргументы, типа того, что "укажите число между ними" не катят, потому что ... ну нет таких чисел, и что? Теоремы-то о том, что между любыми числами есть число, у нас в такой аксиоматике нет...
Как раз, то что это определение не выполняется для данного числа (и для всех с 9 в периоде), это определение можно назвать противоестественным.
Укажите число между ними - "ну нет таких чисел, и что?". Я слышал, что на аксиому Архимеда опирается одна из лемм: между любыми двумя рациональными числами, существует хотя бы одно вещественное.
Мне кажется, лучше ввести определение сравнения числа с 0, и свести то, что a<b к a-b<0.
Так как 0,(9) всё таки равно единице и это доказывается многими способами, то следовательно из 0,(9) и 1 ==> [0,(9)-1 = 0] и 0. Значит знак "=". Конечно теперь можно по-другому ввести отрицание...



