Ну и дискуссия разгорелась...
А слабо было начать с определения отношения порядка для десятичных дробей?
Я, например, не вижу ничего противоестественного в том, чтоба определить так:
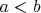
тогда и только тогда, когда старшая несовпадающая цифра у числа

меньше, чем у числа

.
По такому определению

, хотя это и противоречит тому, что
принято в арифметике действительных чисел. Аргументы, типа того, что "укажите число между ними" не катят, потому что ... ну нет таких чисел, и что? Теоремы-то о том, что между любыми числами есть число, у нас в такой аксиоматике нет...