Доказательство Великой теоремы ("по Ферма")

[gris]

Хотя на самом деле я и не собирался нести бред.
С самого начала я просил автора растолковать мне то место, где он утверждает ... ну не буду повторять. Что в этом бредового? Я просил его исправить неточности в написании формул. Разве это свинское поведение? В соседних темах не то же ли самое?

[AD]

gris, думаю, всё правильно Вы делали.

Да и тема убита окончательно ...

[gris]

Но мне не хотелось бы на этом форуме применять методы ведения дискуссий, которыми я, поверьте, в достаточной степени овладел в иных местах интернета и считаю здесь совершенно неприемлемыми. Поэтому в одностороннем порядке прекращаю обсуждение данной темы.

[PAV]

shwedka,
замечание за обсуждение ников

[Мат]

AD
Жалко убивать любую тему. Ведь это труд как-никак человека, который ее создал.

[Brukvalub]

Мат в сообщении #187729 писал(а):

Жалко убивать любую тему. Ведь это труд как-никак человека, который ее создал.

Это, смотря какая у человечишки была цель.... Жажда задешево, ничему не учась, прославиться, к добродетели не отнесешь. Это, однозначно, гордыня, что порицаемо.

[Виктор Ширшов]

Вчера я представил на Ваше обсуждение доказательство ВТФ, полагая, что ВЫ отделите в нём зёрна истины от плевел и шелухи. Нет, Вы погрязли во взаимных оскорблениях, зациклились на знаках неравенства. Вот та истина, спрятанная за словами.
«Считая, что утверждение Ферма распространяется на всю совокупность натуральных чисел, следует предполагать, что он должен был искать исходный посыл для его доказательства в уравнении $z^n=x^n + y^n$. Очевидно, он исследовал его методами спуска и подъёма по схеме n→1→n.
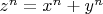
При исследовании Диофантова уравнения «методом спуска», логически рассуждая, приходишь к выводу, что если $z^n = x^n + y^n$, то также $z^{n-1}= x^{n-1}+ y^{n-1}$, $z^{n-2}= x^{n-2}+ y^{n-2)$, ...,$z^{n-m}=x^{n-m} + y^{n-m}$ и наконец, $ z=x+y $.
Исследование уравнения $ z=x+y $ «методом подъёма» показывает, что при $n=2$ равенство превращается в неравенство $z^2 > x^2 + y^2$, так как $x<z>y$. При n=3 знак неравенства сохранится по этому же посылу, т. е. $z^3 > x^3 + y^3$. Далее исследовать каждое последнее неравенство «методом подъёма» – пустая трата времени. И в степени n $z^n > x^n + y^n$».
Почему это решение единственное? Теорема Ферма выводилась на основе Диофантова уравнения $z^n=x^n+y^n$, поэтому всё доказательство должно строиться только из предположения, что $z =x+y$. Случаи, когда $x+y <z<x+y$ здесь не должны рассматриваться.
Ферма утверждал: «$Cubet$ $autem$ $in$ $duos$ $cubos$, $aut$ $quadratoguadratum$ $in$ $duos$ $quadratoguadratos$, $et$ $generaliter$ $nullam$ $infinitum$ $potestatem$ $in$ $duos$ $eiusdem$ $nominis$ $fas$ $est$ $divider$».
В дословном переводе: «Куб, однако, разделить на два куба, или квадрат в квадрате на два квадрата в квадрате, или вообще любую степень до бесконечности больше второй на две степени с тем же обозначением невозможно».
В такой формулировке теорема применима для «пифагоровых троек». Предполагаю, что Ферма умышленно перешагнул через решение (n=2) и сделал он это для того, чтобы отдалить коллег-оппонентов от настоящего решения. Такие «шутки» были в его стиле. Ведь недаром он высказывался, что «если даже математики всего мира потратят целую вечность, чтобы найти решение уравнения, носящего его имя, в целых числах, то и тогда им не удастся найти ни одного решения». Видимо, посчитал, что увёл от правильного пути решения.
Данное доказательство ВТФ изначально не выходит за рамки Диофантова уравнения, распространяется на числа, соответствует условиям теоремы («если x, y, z, n – натуральные числа, то при n>1 $z^n \ne x^n + y^n$ , выполнено с помощью методов Ферма, которые он предлагал применять и, наконец, оно простое. «Я нашёл удивительное доказательство тому, однако ширина полей не позволяет здесь его осуществить», - приписал Ферма к своей теореме. В этом скрытом намёке видится простое и краткое доказательство.

[Brukvalub]

Виктор Ширшов в сообщении #187796 писал(а):

Вчера я представил на Ваше обсуждение доказательство ВТФ

Следует читать: "Вчера я представил на Ваше обсуждение горяченный бред".

Виктор Ширшов в сообщении #187796 писал(а):

Исследование уравнения $ z=x+y $ «методом подъёма» показывает, что при $n=2$ равенство превращается в неравенство $z^2 > x^2 + y^2$, так как $x<z>y$. При n=3 знак неравенства сохранится по этому же посылу, т. е. $z^3 > x^3 + y^3$. Далее исследовать каждое последнее неравенство «методом подъёма» – пустая трата времени. И в степени n $z^n > x^n + y^n$».

Вот читать этот бред - это уж точно "пустая трата времени".

[Виктор Ширшов]

«Если даже математики всего мира потратят целую вечность, чтобы найти решение уравнения, носящего его имя, в целых числах, то и тогда им не удастся найти ни одного решения».

ОСТРОСЛОВЫ, ПУСТОСЛОВЫ и ЗЛОСЛОВЫ! Вы вдумайтесь в эти слова. Заметьте, это не я сказал, а Ферма. Если изначально выбран неправильный путь доказательства, никогда не найти решения. А он его подсказал.

[Коровьев]

Мат писал(а):

Жалко убивать любую тему. Ведь это труд как-никак человека, который ее создал.

Може и за котом не надо убирать из-под кровати? Как-никак, трудился...

[Yarkin]

Виктор Ширшов в сообщении #187796 писал(а):

Вчера я представил на Ваше обсуждение доказательство ВТФ, полагая, что ВЫ отделите в нём зёрна истины от плевел и шелухи. Нет, Вы погрязли во взаимных оскорблениях,

Никаких взаимных оскорблений нет. Вы попали под математический юмор. Со мной такую игру провела shwedka. А я Вас предупреждал. Дам еще два совета. Можете и их проигнорировать. 1. Познакомится с материалами Форума на эту тему. В них Вы найдете все Ваши неравенства не только с подъемом и спуском, но и без них. 2. Познакомится с Античной эстетикой Лосева.

[Коровьев]

Вот ведь как получается, как только bot дал абсолютно верную формулирофку БТФ в терминах неравенств

bot писал(а):

Ладно, дарю Вам переформулировку ВТФ в терминах неравеств.

Если $x, y, z, n$ - целые положительные числа и $n>2$, то либо

$x^n+y^n < z^n$

либо

$x^n+y^n > z^n$

так сразу оказалось, что доказывает-то автор темы то, что уже задано как условие!
Отсюда и это

Виктор Ширшов в сообщении #187796 писал(а):

Случаи, когда x+y<z<x+y здесь не должны рассматриваться

А иначе а что ж - нет доказательства? Ну и тут, ессественно, вместо изучения своих ошибок начинается цитирование Великих из прошлого, как доказательство своей правоты.
А иначе а что ж.

[Виктор Ширшов]

Коровьёв писал: "Вот ведь как получается, как только bot дал абсолютно верную формулирофку БТФ в терминах неравенств..."
Ферма пишет: "...и вообще любую степень до бесконечности больше второй..." . Если рассматривать такую фомулировку теоремы Ферма и формулировку, данную участником под ником "bot для неравенств, доказательство должно строиться из предположения, что $z^2 = x^2+ y^2$, т. е. распространить его только на "пифагоровы тройки", и выполнить на примере прямоугольного треугольника. В формулировке на латинском языке о квадратах речи нет. Найдите в записи "$et$ $generaliter$ $nullam$ $infinitum$ $potestatem$ $in$ $duos$ $eiusdem$ $nominis$ $fas$ $est$ $divider$» слово $.
К сказанному добавлю, что Ферма исследовал Диофантово равенство, в которое при n=1 пифагоровы тройки не вписываются.
Добавлено спустя 26 минут 36 секунд:

И ещё. Все доказательства теоремы Ферма строятся из предположения n>2, на которое указывает Ферма. Но при исследовании уравнения Диофанта «методом спуска» равенство $z^2 = x^2 + y^2$ не последнее, а есть ещё $z=x+y$, от которого отделяет всего одно решение "методом спуска": если есть равенство $z^2 = x^2 + y^2$, то есть и меньшее.
Извините за тавтологию, но она иногда помогает, так как некоторым надо очень долго вдалбливать.

[Brukvalub]

Тогда идите получать Большую Золотую Медаль как Перворешатель ВТФ.
А лукчше, идите на уколы, вас там процедурная сестра заждалась!

[Виктор Ширшов]

Brukvalub в сообщении #187799 писал(а):

Следует читать: "Вчера я представил на Ваше обсуждение горяченный бред".

Если здесь такой "горяченный бред", тогда что же Вы тут торчите.