Доказательство Великой теоремы ("по Ферма")

[Руст]

gris писал(а):

Меня поразила одна мысль.
Может быть ВТФ потому и не поддаётся, что все пытаются доказывать её на современном алгебраическом языке?

Как раз на современном алгебраическом языке она уже доказана.

Цитата:

А если хорошенько подучить латынь и поговорить с Теоремой, как это делал сам Ферма?
Вдруг его доказательство, простое на словах, вообще не может быть записано современной нотацией?

Сам Ферма и последователи до Уайлса не доказали. То, что Ферма не доказал, говорит уже тот факт, что после известного писания на полях, что он нашёл доказательство, через 6 лет он всё таки опубликовал доказательство частного случая для $n=4$. К тому же он делал и другие ошибочные бездоказательные утверждения, например о простоте всех чисел $2^{2^n}+1$.

Цитата:

И ещё. Можно подумать, что в соседней конкурирующей теме, которую мы обогнали по числу страниц, обсуждается более правдоподобное доказательство.

В математике пользуются чёткой логикой, где не бывает, более правдобподобных доказательств. Они или истинны, или нет. Т.е. истинность принимает только два значения.

[Виктор Ширшов]

gris в сообщении #187293 писал(а):

Дискуссию можно закрывать.

Рано ещё. Ведь, развёрнутого, логически построенного доказательства я Вам не дал: только фрагмент. В противном случае, дисскутировать было бы не о чем.

[bot]

Руст писал(а):

То, что Ферма не доказал, говорит уже тот факт, что после известного писания на полях, что он нашёл доказательство, через 6 лет он всё таки опубликовал доказательство частного случая для $n=4$.

Этот случай конечно важен, поскольку позволяет ограничиться случаями простых показателей, однако случай n=3 Ферма ведь пропустил ...
А не потому ли пропустил, что он значительно сложнее и требовал принципиально новых идей, породивших целое направление?

[gris]

Ага. Так Вы же сами написали в первом посте

Виктор Ширшов писал(а):

Отсюда следует, что $z^n \ne x^n + y^n$ при $n \ne 2$.
Таким образом, утверждение Ферма ...доказано.

Так это был только фрагмент:(

Представляю, через сколько страниц мы подберёмся к рассмотрению хотя бы второго пункта...

[Виктор Ширшов]

bot в сообщении #187298 писал(а):

Если целые, и , то .

.
К чему все эти Ваши абстракции? Теорему Ферма решают более 350 лет, а Вы от меня хотите сразу получить решение вашего примера.
Тем не менее, если $xyz=0$, то в этом случае, как минимум, один сомножитель должен равняться числу 0, который согласно определению:" Одна из единиц в записи числа, означающая отсутствие единиц данном разряде".
Пусть х=0. В этом случае Диофантово уравнение приобретает вид - $z^n=0+y^n = y^n$. И какое отношение это имеет к формулировке Ферма, где одно целое число надо разложить на два целых числа с таким же показателем.

[bot]

Не понимаю, о каком таком втором пункте речь?
Если действительно "утверждение Ферма доказано", то обсуждать больше нечего.
Если же этот фрагмент ошибочен, то получается как в присказке про колы и мочала, чем собссно и занимаемся.
Имхо, тему пора закрывать, а то какая-то недержимость речи наблюдается - я и к себе это отношу.

Добавлено спустя 2 минуты 19 секунд:

Виктор Ширшов в сообщении #187336 писал(а):

К чему все эти Ваши абстракции? ...

Всё, с меня довольно.

[Виктор Ширшов]

gris в сообщении #187333 писал(а):

Представляю, через сколько страниц мы подберёмся к рассмотрению хотя бы второго пункта...

.
Много страниц не будет.
Я его представлю сегодня вечером, в 21 час по московскому времени.

[tolstopuz]

Виктор Ширшов писал(а):

числу 0, который согласно определению:" Одна из единиц в записи числа, означающая отсутствие единиц данном разряде".

Число - это одна из единиц в записи числа. Я в восхищении!

[Yarkin]

Виктор Ширшов в сообщении #187339 писал(а):

Я его представлю сегодня вечером, в 21 час по московскому времени.

Не торопитесь. У Вас еще нет четкой формулировки того, доказательство чего Вы хотите дать.

[Мат]

Виктор Ширшов писал(а):

Я уже сказал, что настольной книгой Ферма были «Начала» Евклида, в которой изложено учение пифагорейцев, находившихся «в плену числа». Они всегда стремились к точному обоснованию своих математических утверждений и делали это с помощью геометрических образов. Две точки определяли у них прямую линию, одномерный образ; три точки, не лежащие на одной прямой, - треугольник или плоскость – двумерный образ; четыре точки, не лежащие на одной плоскости – пирамиду – трёхмерный образ.

"Быть может, потомки будут признательны мне за то, что я показал, что древние знали не все."
П.Ферма.

Добавлено спустя 9 минут 9 секунд:

Попробуйте проанализировать с помощью вашего метода уравнение $x^n+y^n=z^k, k\neq n$. Что получится?

[gris]

Конкурирующая фирма пожаловала. Почём опиум для народа?

[Brukvalub]

Виктор Ширшов в сообщении #187327 писал(а):

Рано ещё. Ведь, развёрнутого, логически построенного доказательства я Вам не дал: только фрагмент. В противном случае, дисскутировать было бы не о чем.

Виктор Ширшов в сообщении #187339 писал(а):

Много страниц не будет.
Я его представлю сегодня вечером, в 21 час по московскому времени.

Минута славы продолжается!
Настоящих буйных в теме прибавляется!
К вечеру ожидается развлекуха "по полной программе"!
Итак, только в нашем цирке, и только сегодня вечером прыжок из-под купола без страховки с приземлением голой задницей в бочку с опилками и ржавым гвоздем в середине!
Публика в нетерпении ждет-с! :
Алле-опп!

[Виктор Ширшов]

Итак, сформулированная теорема сводится к неравенству $z^n$ $\ne$ $x^n+y^n$ при n$\ne$2, где x, y, z – целые числа.
ВТФ читается следующим образом: «Ни куб на два куба, ни квадрато-квадрат, и вообще никакая степень, кроме квадрата, не может быть разложена (нельзя разложить, значит, нельзя поставить знак равенства – В.Ш.) на сумму таких же».
Из этого расплывчатого утверждения можно сделать двоякий вывод: либо x, y, z - это только «пифагоровы тройки» в целых натуральных числах, либо это все целые натуральные числа от 1 до n.
Доказательство Великой теоремы Ферма выполнил с помощью «метода подъёма»: «Для доказательства нерешаемости в целых числах уравнения с разложением на два слагаемых в той же степени мы предлагаем метод, противоположный ранее предложенному нами методу спуска, с помощью которого нам удалось обогатить математику целых чисел. Предлагаемое же доказательство сформулированной нами теоремы разложения степеней основывается на методе подъёма (подчёркнуто В. Ш.)».
В последующем математики не поняли, что подразумевал Ферма за этой «литературной условностью» (сам он не разъяснил сути «метода подъёма», и предположили, что он ошибся в «удивительном доказательстве» Великой теоремы, а ошибка кроется именно в нём.
Хотя Ферма не раскрыл метода доказательства теоремы, однако всё же можно догадаться, что его следует проводить способом подъёма степеней, то есть исследовать Диофантово уравнение в порядке подъёма степеней (от 1 до n).
Доказательство теоремы Ферма для «пифагоровых троек» можно выполнить на примере прямоугольного треугольника, как геометрической записи того, что выражается словами.
а) в первой степени уравнение $z^n= x^n + y^n$ фактически сводится к сумме двух чисел (геометрических отрезков). Так как в любом треугольнике одна сторона меньше двух других сторон (строгое неравенство треугольника), в первой степени Диофантово уравнение – неравенство: $z < x+y$;
б) в квадрате исследуемое уравнение принимает вид Пифагорова равенства, так как в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Во времена Диофанта, а тем более Ферма, это уже не надо было доказывать - $ z^2 = x^2+ y^2$;
в) в кубе равенство снова становится неравенством, причём, знак неравенства меняется на противоположный. Из теоремы Пифагора следует, что в прямоугольном треугольнике любой из катетов меньше гипотенузы: $x<z>y$. Поэтому будет неоспоримым авторское утверждение о том, что правая часть Диофантова выражения будет меньше левой, так как в правой части каждое из двух возводящихся в куб чисел (x,y) будет меньше куба третьего числа(z). Это утверждение справедливо на том основании, что равенство сохраняется только в том случае, если обе его части умножить на одно и то же число (одно из свойств равенств). Таким образом, при $n =3$ и $x<z>y$, равенство $z^2 = x^2 + y^2$ приобретает вид неравенства $z^3>x^3 + y^3$;
г) в четвёртой степени («квадрато-квадрате» или «биквадрате») неравенство сохранится в силу одного и того же свойства, общего со свойством равенства: неравенство сохраняется, если обе его части умножить на одно и то же число. При n=4 неравенство $z^4 >x^4+ y^4$ совершенно очевидно, так как $x<z>y$;
д) в пятой и во всех последующих степенях, вплоть до n-й степени Диофантово уравнение будет неравенством.
Отсюда следует, что $z^n $\ne$ x^n + y^n$ при n$\ne$2.
***
Считая, что утверждение Ферма распространяется на всю совокупность целых натуральных чисел, надо предполагать, что он должен был искать исходный посыл для доказательства в уравнении $z^n=x^n + y^n$. Очевидно, он исследовал его по схеме Ферма n→1→n: сначала посредством «метода спуска», а затем «методом подъёма».
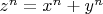
При исследовании Диофантова уравнения «методом спуска», путём логических рассуждений приходишь к выводу, что если $z^n = x^n + y^n$, то также $z^{n-1} = x^{n-1}+ y^{n-1}$, ..., $z^{n-m} = x^{n-m} + y^{n-m}$, и наконец, $z=x+y$.
1. Исследование уравнения $ z=x+y$ «методом подъёма» степеней показывает, что при n=2 равенство превращается в неравенство $z^2 > x^2 + y^2$, так как $x<z>y$. При n=3 знак неравенства сохранится по этому же посылу, т. е. $z^3 > x^3 + y^3$. Далее исследовать каждое последнее неравенство «методом подъёма» – пустая трата времени. И в степени n $z^n > x^n + y^n$.
В данное доказательство не вписываются «тройки чисел», в которых $ z>x+y $ и $ z<x+y $.
2. С помощью «метода подъёма» устанавливается справедливость утверждения Ферма для неравенства $ z>x+y $, которое при n=2,3,…,n-m,…, наконец, n, останется неравенством со знаком «>», т. к $x<z>y$.
3. «Тройки чисел», когда $z<x+y $ представимы на плоскости треугольниками. Для «пифагоровых троек» справедливость утверждения Ферма доказывалась на примере прямоугольного треугольника. Для других четырёх возможных случаев, отвечающих условию $z<x+y$, в которых числа сопоставимы со сторонами треугольников (остроугольный, равнобедренный, равносторонний и тупоугольный), доказательство выполняется «методом подъёма» по схеме, как и для «пифагоровых троек». В трёх случаях перемены знака неравенства не происходит и только в одном (тройки, образующие остроугольный треугольник), в котором x и y незначительно разнятся с z, она происходит и только с > на <.

[gris]

Первыйна...
Для пифагоровых троек теорема верна.

[ZheniaM]

Боже....какой бред

Не мог удержаться и не написать