Доказательство Великой теоремы ("по Ферма")

[Brukvalub]

Виктор Ширшов в сообщении #188217 писал(а):

Я уже просто не знаю, как вталдычить недогоняющим, что изначальным пунктом доказательства ВТ должна быть просто сумма двух натуральных чисел.
В рамках Диофантова уравнения Ферма должен был сформулировать ВТ следующим образом: " Дифантово равенство, выражаемое целым натуральным числом с целочисленным показателем, кроме квадрата (частный случай решения в "пифагоровых тройках"), нельзя разложить на два целых числа с таким же показателем".
Почему он так не сделал? Чтобы затруднить поиски правильного решения своим ненавистным оппонентам. Ведь, в такой формулировке, кому-нибудь пришла бы в голову мысль начать исследование с $z = x+y$.

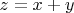
А и не нужно ничего нам вталдычвать, втюхивать, впаривть, подсовывать, и т.д.
Мы этих "дурилок картонных" и без вас немало видывали.
Просто вы не можете найти решение ВТФ в правильной формулировке, и решили всех обдурить, приписывая Ферма некую другую формулировку, которая, как вам кажется, легче поддается исследованию.
Дудки, никого здесь этой подменой не разжалобишь.
В конечном счете, есть стандартная формулировка ВТФ, решение которой оказалось очень непростым делом, а что там на самом деле думал именно Ферма, теперь интересует лишь историков математики. Вот им и "парьте мозги", изображая из себя Перворешателя ВТФ.
Знали бы вы, как здесь всем надоели безграмотные неучи, вроде вас, которые снедаемы похотью задешево прославиться и прослыть великими математиками.
Зарубите себе на носу и остальных частях тела: чтобы стать математиком, мало знать формулу корней квадратного уравнения, бином Ньютона и прочие тривиальности.
Для этого нужно, как минимум, лет 8-10 интенсивно учиться, отдавая этому все свои силы, сдать немало экзаменов и зачетов, прочесть уйму учебников, монографий и периодических изданий, поучаствовать в работе нескольких научно-исследовательских семинаров, поучиться уму-разуму у научного руководителя, сделать несколько самостоятельных научных исследований в математике, которые будут признаны достойными публикации и опубликованы, написать и защитить одну или две диссертации.
Вот пойдите и поучитесь, вместо того, чтобы подменять Великие Задачи своей суррогатной ахинеей. А сделать с кондачка Великое Открытие в той единственной понятной вам с вашими убогими знаниями области математики, вам все равно не удастся - это показывает многовековой опыт.
Как-то вот так получается....

[Someone]

Виктор Ширшов, я хотел бы видеть Ваши комментарии по поводу вот этого:

Виктор Ширшов в сообщении #188138 писал(а):

Хорошо, пусть при n=2 $z^2 = x^2 + y^2$. Но тогда и при n=1 z=x+y.

Someone в сообщении #188158 писал(а):

Хорошо, пусть при $n=2$ $5^2=3^2+4^2$. Но тогда и при $n=1$ $5=3+4$.

Виктор Ширшов в сообщении #188228 писал(а):

Когда Вы поймёте, что надо доказывать исходя из z=x+y, говорить будет уже не о чем

Пока Ваше заявление в первой цитате выглядит верхом идиотизма: для пифагоровых троек $x,y,z$ равенство $z=x+y$ неверно. Точно так же оно неверно для гипотетических положительных целочисленных решений уравнения $z^n=x^n+y^n$ при $n>2$, поэтому рассматривать числа, удовлетворяющие равенству $z=x+y$, совершенно бессмысленно.

[Виктор Ширшов]

Someone в сообщении #188365 писал(а):

Пока Ваше заявление в первой цитате выглядит верхом идиотизма: для пифагоровых троек равенство неверно.

Наконец-то, задумались. А то я уж подумал, что на форуме только любители Шукшина и сарказма.
Вы абсолютно правы. И поэтому я вношу поправку в свою формулировку ТФ:"Диофантово равенство, выраженное целым натуральным числом с целочисленным показателем, в степени n >1 нельзя разложить на два целых числа стаким же показателем".

[shwedka]

Виктор Ширшов в сообщении #188391 писал(а):

Диофантово равенство, выраженное целым натуральным числом с целочисленным показателем, в степени n >1 нельзя разложить на два целых числа стаким же показателем

Как-то у Вас с языком плохо. Вы пытаетесь РАВЕНСТВО разложить на ЧИСЛА. Я могу представить себе как можно число разложить (в сумму или, скажем, произведение) чисел. Но равенство? разложить??
И как это РАВЕНСТВО выражается ЧИСЛОМ??

Может, попробуете подумать, так, для тренировки.

[Виктор Ширшов]

shwedka в сообщении #188398 писал(а):

Как-то у Вас с языком плохо. Вы пытаетесь РАВЕНСТВО разложить на ЧИСЛА

А так: "Целое натуральное число с целочисленным показателем в степени n>1 нельзя разложить на два целых числа с таким же показателем".

[shwedka]

Уже лучше. Вот если еще $n>1$ замените на $n>2$ и замените 'разложить на два целых числа' на 'разложить в сумму двух натуральных положительных чисел' , то совсем здорово будет.

[Yarkin]

Виктор Ширшов в сообщении #188403 писал(а):

А так: "Целое натуральное число с целочисленным показателем в степени n>1 нельзя разложить на два целых числа с таким же показателем".

Я предупреждал, что у Вас нет четкой формулировки того, что Вы хотите доказать, И снова, советую не торопиться. В предлагаемой формулировке игнорируются пифагоровы тройки.

[Виктор Ширшов]

shwedka в сообщении #188411 писал(а):

Уже лучше. Вот если еще замените на и замените 'разложить на два целых числа' на 'разложить в сумму двух натуральных положительных чисел' , то совсем здорово будет.

Заменять n>2 на n>1 не буду. А Ваше словосочетание приму "Целое натуральное число с целочисленным показателем в степени n>1 невозможно разложить в сумму двух натуральных чисел".

[AV_77]

Виктор Ширшов писал(а):

Целое натуральное число с целочисленным показателем в степени n>1 невозможно разложить в сумму двух натуральных чисел.

Это как?

PS $5^2 = 9 + 16$

[Виктор Ширшов]

Yarkin в сообщении #188412 писал(а):

Я предупреждал, что у Вас нет четкой формулировки того, что Вы хотите доказать, И снова, советую не торопиться. В предлагаемой формулировке игнорируются пифагоровы тройки.

Пифагоровы тройки - решение для неравенства $z^n < x^n + y^n$, но не для Диофантова уравнения, на которое, не задумываясь, "клюнули".

Добавлено спустя 14 минут 40 секунд:

AV_77 в сообщении #188421 писал(а):

Виктор Ширшов писал(а):
Целое натуральное число с целочисленным показателем в степени n>1 невозможно разложить в сумму двух натуральных чисел.

В этом Вы, shwedka и Ферма правы: "Целое натуральное число с целочисленным показателем n>2 невозможно разложить в сумму двух натуральных чисел с тем же показателем"

[Yarkin]

Виктор Ширшов писал(а):

[ Пифагоровы тройки - решение для неравенства $z^n < x^n + y^n$, но не для Диофантова уравнения, на которое, не задумываясь, "клюнули".

Следовательно, $x^2+y^2=z^2$ - не диафантово уравнение?

[Виктор Ширшов]

Yarkin в сообщении #188432 писал(а):

Следовательно, - не диафантово уравнение?

Смотри предыдущее сообщение, я поправил.

[Yarkin]

Виктор Ширшов в сообщении #188438 писал(а):

Смотри предыдущее сообщение, я поправил.

Мы стали друзьями и перешли на "ты"?

[Алексей К.]

Виктор Ширшов в сообщении #188234 писал(а):

Я уже всё сказал. Дальше я дисскутировать не буду.

[Виктор Ширшов]

Yarkin в сообщении #188442 писал(а):

Мы стали друзьями и перешли на "ты"?

Извините.