Решила её методом алгебраического сложения.
Повторите метод алгебраического сложения. Он не в том состоит, что надо просто сложить или вычесть уравнения и всё.
Вам надо бы разобраться, что преобразования уравнений и их систем бывают равносильные и неравносильные.
Вот, например, равенство

равносильно равенству

. Это значит, что из первого равенства можно вывести второе, а из второго - вывести первое. Из

можно получить

, если вычесть

из левой и правой части. Типа, если

и

- это одно число, то и после вычитания двойки получатся одинаковые результаты:

, т.е.

. Наоборот, из

можно получить

, если прибавить

к левой и правой части.
Вот пример неравносильных равенств:

и

. Из первого равенства следует второе: если

, то

. Но из второго равенства не следует первое: если

, то ещё не факт, что

; может быть и так, что

.
Решая уравнение или систему уравнений, лучше всего пользоваться только равносильными преобразованиями. Если делать неравносильные, то можно получить "лишние" корни: как корень

в предыдущем примере.
Так вот, сложение уравнений системы - это неравносильное преобразование. Вы сделали правильный вывод, что

, и Вы правы в том, что уравнение Вашей прямой должно иметь вид

. Но Вы не нашли эти

и

- а если бы постарались, могли бы их найти (с точностью до общего множителя) и получить то, что в ответе.
Неравносильные преобразования при решении задач допустимы, но нужно помнить, что они могут приводить к "лишним" решениям.
Как понять, преобразование равносильное или нет? Только думать. Вот, например, если

и

, то отсюда можно сделать вывод, что

. Но если нам дано, что

, то отсюда нельзя вывести, что

и

- может ведь быть ещё например так, что
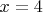
, а

. Так что сложение уравнений - не равносильное преобразование.
Это Вам просто материал для размышлений. А конкретно по задаче - изучите подробнее, как решаются системы уравнений.



