Пусть имеется множество

где

. Тогда, если

является аддитивной группой, то вместе с двумя элементами множества

и

ему принадлежит также их разность (

).
Любой элемент множества

можно представить как конечную сумму разностей соседних элементов

Попробуем выяснить структуру элементов множества

. Для этого рассмотрим его при первых значениях

.
При

получим
![$$\[ \genfrac{}{}{0pt}{}{\pmb 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \dots}
{0\ \ \ 0\ \ \ 0\ \ \ 0\ \ \ 0\ \ \ 0\ \dots} \qquad \]$$ $$\[ \genfrac{}{}{0pt}{}{\pmb 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \dots}
{0\ \ \ 0\ \ \ 0\ \ \ 0\ \ \ 0\ \ \ 0\ \dots} \qquad \]$$](https://dxdy-02.korotkov.co.uk/f/d/e/e/dee6f616e9378edf90b6d01fc577dcb682.png)
Разности обратились в

на первом шаге.
Обратите внимание на первые элементы ненулевых строк – они являются ключевыми для определения искомой структуры.
При

получим
![$$\[ \genfrac{}{}{0pt}{}{\pmb 1\ \ \ 2\ \ \ 3\ \ \ 4\ \ \ 5\ \ \ 6\ \ \ 7\ \dots}
{\pmb 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \dots} \qquad \]
\[ \genfrac{}{}{0pt}{}{0\ \ \ 0\ \ \ 0\ \ \ 0\ \ \ 0\ \dots}{} \qquad \]\\$$ $$\[ \genfrac{}{}{0pt}{}{\pmb 1\ \ \ 2\ \ \ 3\ \ \ 4\ \ \ 5\ \ \ 6\ \ \ 7\ \dots}
{\pmb 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \ \ 1\ \dots} \qquad \]
\[ \genfrac{}{}{0pt}{}{0\ \ \ 0\ \ \ 0\ \ \ 0\ \ \ 0\ \dots}{} \qquad \]\\$$](https://dxdy-02.korotkov.co.uk/f/5/c/5/5c5c3dc46e8b9bc1fafbc1dfea36a7ac82.png)
Разности обратились в

на втором шаге. Можно ожидать, что для

это произойдёт на третьем шаге. Проверим.
При

получим
![$$\[ \genfrac{}{}{0pt}{}{\pmb 1\ \ \ 4\ \ \ 9\ \ \ 16\ \ \ 25\ \ \ 36\ \ \ 49\ \dots}
{\pmb 3\ \ \ 5\ \ \ 7\ \ \ 9\ \ \ 11\ \ \ 13\ \dots} \qquad \]
\[ \genfrac{}{}{0pt}{}{\pmb 2\ \ \ 2\ \ \ 2\ \ \ 2\ \ \ 2\ \dots}
{0\ \ \ 0\ \ \ 0\ \ \ 0\ \dots} \qquad \]\\$$ $$\[ \genfrac{}{}{0pt}{}{\pmb 1\ \ \ 4\ \ \ 9\ \ \ 16\ \ \ 25\ \ \ 36\ \ \ 49\ \dots}
{\pmb 3\ \ \ 5\ \ \ 7\ \ \ 9\ \ \ 11\ \ \ 13\ \dots} \qquad \]
\[ \genfrac{}{}{0pt}{}{\pmb 2\ \ \ 2\ \ \ 2\ \ \ 2\ \ \ 2\ \dots}
{0\ \ \ 0\ \ \ 0\ \ \ 0\ \dots} \qquad \]\\$$](https://dxdy-03.korotkov.co.uk/f/2/1/c/21c860ad95e9008e07cb6c4caaa4290d82.png)
Предположение было верным.
При

получим
![$$\[ \genfrac{}{}{0pt}{}{\pmb 1\ \ \ 8\ \ \ 27\ \ \ 64\ \ \ 125\ \ \ 216\ \ \ 343\ \dots}
{\pmb 7\ \ \ 19\ \ \ 37\ \ \ 61\ \ \ 91\ \ \ 127\ \dots} \qquad \]
\[ \genfrac{}{}{0pt}{}{\pmb 12\ \ \ 18\ \ \ 24\ \ \ 30\ \ \ 36\ \dots}
{\pmb 6\ \ \ 6\ \ \ 6\ \ \ 6\ \dots} \qquad \]
\[ \genfrac{}{}{0pt}{}{0\ \ \ 0\ \ \ 0\ \dots}{} \qquad \]\\$$ $$\[ \genfrac{}{}{0pt}{}{\pmb 1\ \ \ 8\ \ \ 27\ \ \ 64\ \ \ 125\ \ \ 216\ \ \ 343\ \dots}
{\pmb 7\ \ \ 19\ \ \ 37\ \ \ 61\ \ \ 91\ \ \ 127\ \dots} \qquad \]
\[ \genfrac{}{}{0pt}{}{\pmb 12\ \ \ 18\ \ \ 24\ \ \ 30\ \ \ 36\ \dots}
{\pmb 6\ \ \ 6\ \ \ 6\ \ \ 6\ \dots} \qquad \]
\[ \genfrac{}{}{0pt}{}{0\ \ \ 0\ \ \ 0\ \dots}{} \qquad \]\\$$](https://dxdy-04.korotkov.co.uk/f/7/1/2/712b97945ebba968993b31e6ed50916a82.png)
Для наших целей этого будет достаточно.
Далее, соберём элементы множества

из полученных разностей.
При

все разности, а значит и любая их сумма, равны

, поэтому, любой элемент множества

равен его первому элементу – единице.
При




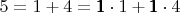
и так далее. Обратите внимание на выделенные коэффициенты.
При






Этого достаточно, чтобы заметить – любой элемент множества

можно собрать из указанных выше первых элементов ненулевых строк

. Также можно видеть, что коэффициенты при них принадлежат первым строкам треугольника Паскаля

при этом, номер элемента в множестве одновременно является номером строки треугольника Паскаля.
В случае

коэффициенты при элементах

лежат в первых двух столбцах треугольника Паскаля

а в случае

коэффициенты при элементах

лежат в первых четырёх столбцах

Таким образом, элементы множества

можно рассматривать как значения скалярных произведений


где вектор

является строкой треугольника Паскаля (

-треугольника) и отвечает за основание степени, а вектор

является строкой

-треугольника

и отвечает за показатель степени.

-треугольник, подобно треугольнику Паскаля, можно построить пользуясь рекурентной формулой


-треугольник находится в тесной связи с числами Стирлинга

-го рода, но далее я покажу, что ещё более тесно он связан с треугольником Паскаля.
Мы выяснили, что элементы множества

имеют структуру скалярного произведения в котором сомножителями выступают векторы принадлежащие упорядоченным множествам. Пользуясь этим, условие аддитивности

можно записать в матричном виде
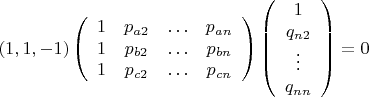 Отступление о родстве
Отступление о родстве  и
и  треугольников.
треугольников.
Элемент треугольника Паскаля, по определению, составлен из элементов вышележащей строки. Но мы оперируем не элементами, а целыми строками или их частями. Возникает естественный вопрос – а можно ли строку целиком получить из другой строки? Иначе говоря, можно ли указать оператор действие которого на строку (ведь мы понимаем её как вектор) даст другую строку? Такой оператор указать можно. Вот его матрица

Действие степени этого оператора на первый орт даст строку треугольника Паскаля с номером на

меньшим этой степени.
Но оказывается, что

-треугольник можно построить совершенно так же с той разницей, что лента матрицы оператора будет содержать не первый столбец треугольника Паскаля, а его второй столбец

Возникает очевидное желание продолжить построение треугольников операторами образованными при помощи следующих столбцов треугольника Паскаля. Это приводит к тому, что простые числа (не знаю – все ли, мне известно уже больше сотни) оказываются представимы скалярными произведениями по указанной схеме.
Но это уже другая история.
Продолжение следует.



