Помогите, пожалуйста. Никак не могу понять, что он хотел показать в задаче 15.1:
Вычислмть определитель  путем возведения его в квадрат.
путем возведения его в квадрат.Во-первых, непонятно, умножение на какой вообще определитель задумывалось для решения этой задачи, ибо в указании сказано следующее:
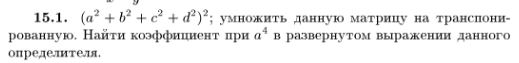
И вот то ли его умножать на себя, а то ли на транспонированный. Так мало того, в указании сказано
Цитата:
Найти коэффициент при

в развернутом выражении данного определителя
Это тоже сбивает с толку: если у меня будет развернутое выражение данного определителя, то зачем для вычисления мне его еще умножать на что-то там еще? Это ведь ошибка в указании?
А пока давайте рассмотрим оба предложенных варианта для вычисления данного определителя. Если предположить, что имелось ввиду возведением в квадрат, то получаем:


. Полученный определитель не выглядит таким уж простым для своего вычисления, да и задачи такого типа обычно не про это. В таких задачах обычно ожидаешь получение какого-нибудь верхнетреугольного или нижнетреугольного определителя, у которого перемножение элементов, стоящих на соответственной для данного случая диагонали, не вызывает каких-либо затруднений, как правило, даже в уме. Теперь попробуем умножение на транспонированный:


. Уже как бы проще, но... Из этого равенства получаем, что квадрат исходного определителя равен

. Это, конечно, хорошо, только вот, как теперь узнать, чему равен исходный определитель:

или

? У меня почему-то идей нет. Или это неправильно сформулированное задание? В задачнике Фаддеева, Соминского в задачах подобного плана требуется вычислить квадрат определителя, но не сам определитель.



