Для первого уравнения системы
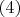
годится параметризация

Имеются варианты. Значит, можно выписать

-х параметрическое решение слабого кубоида, но очень уж оно длинное. Если оно к тому же и общее, то сильный кубоид неразрешим. Всё дело в простеньком на вид уравнении

, с которым сталкиваешься всю дорогу, размышляя над этой задачей. Можно его переписать так

, или записать в систему

, из которой решения

следуют напрямую:

. Общее решение первого уравнения системы

выражается тождеством

. Чтобы произведение внутренних скобочек

оказалось квадратом, достаточно решить уравнение

Оно также инвариант

(достаточно разделить скобки на

), ничего нового написать так и не удается. Но в таком виде удается найти

-параметрическое решение:

, откуда и получаем решение слабого кубоида. Заметим, что система
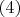
похожа на систему из двух уравнений с двумя неизвестными, если забыть, что под квадратами правой части скрываются еще две переменные. Любые попытки её решения на основе полученных формул неизменно приводят к уравнению с одним неизвестным. Решения такого уравнения выражаются не буквами, а конкретными числами. Даже если повезет, и они будут целыми, кубоид окажется уникальным. Такое бывает, но скорее всего оно из чисел

, иначе проект yoyo@home давно бы его засёк. Совсем иная ситуация сложилась бы, если решение

было бы

-x параметрическим, такого пока не вижу. Да и есть ли оно?