Итак,
доказательство 2 (первое было
здесь).
Имеем уравнение

и тождество


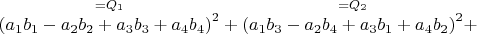

Для начала выясним, возможно ли привести в строгое соответствие элементы одного и другого, чтобы в последствии с помощью

найти общее решение

Представим на минуту

в качестве уравнения, приравняв выражения в скобочках к параметрам в надстрочниках, и выясним условия его разрешимости, т.е. ответим на вопрос какими еще свойствами должны обладать параметры

кроме видимого свойства равенства сумм четырех квадратов. Запишем две линейных системы из четырех уравнений относительно

:

и приравняем решения:

У равных дробей с равными знаменателями равны так же и числители. Приравнивая их попарно, получаем однородную систему относительно

:

Определитель такой системы

должен равняться нулю, что является необходимым и в общем случае достаточным условием разрешимости

Сумма квадратов рациональных чисел даже с минусом может быть

только, если основания квадратов

Для первого квадрата это выполняется по уже известному свойству, остается проверить второй:
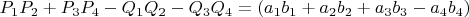




Выполняется тождественно, как и первое, что отличает форму

от формулы Эйлера и делает ее максимально пригодной для описания уравнения

проведя соответствие

видим, что условия разрешимости

вполне соответствуют свойствам

:

(первое выполняется по умолчанию). Иными словами, все решения

, если они имеются, могут быть описаны формой (10). Запишем:

Далее копирую доказательство

с изменениями в индексах и названиях букв.
Складывая и вычитая почленно уравнения

, получаем:

Домножая на
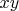
, имеем

(


-е и

-е уравнения)

По той же схеме

Домножая на

:


Решая два новых уравнения относительно

и приравнивая результаты, получаем:


Предпоследняя дробь получена из двух предыдущих почленным вычитанием числителей и знаменателей, что для равных дробей позволено. Далее из

следует

. Подставляя это в уравнение

, получаем

, откуда

Перпишем теперь уравнение

так:

Если бы в

вместо единиц стояли минус единицы, получили бы из последней подстановки

без потери общности, и третьего не дано. Ну, а при

решение известное:

Ранее было показано, что уравнение

равносильно задаче о Диофатовом кирпиче. Если бы последнее имело ненулевые решения, то для любых рациональных

нашлись бы тройки

такие, что

в том числе и для

. Тогда получили бы нетривиальное решение уравнения

, где оба параметра

отличны по модулю от единицы. Но общее решение

таково:

Это было доказано выше и противоречит предположению. Значит, его не существует.