Ну вот, теперь почти всё правильно. Начало у Вас уже очень хорошее, только желательно в законе сохранения импульса всегда записывать скорости как векторы (чтобы потом было понятнее, что такое разность или сумма скоростей):


Скорость системы как целого

давайте пока не будем использовать. Перепишем закон сохранения энергии, перенеся конечную кин. энергию Земли из правой стороны в левую сторону. Тогда в левой стороне образуется разность начальной и конечной кин. энергии Земли (записываю её в скобках):

Подставим в неё выражение для конечной скорости Земли; оно следует из закона сохранения импульса:

Тогда для разности кин. энергий Земли имеем (у Вас получилось похожее выражение, но без векторных обозначений и со скоростью

вместо

):

Важно, что здесь обнаружилось слагаемое

которое не зависит от массы Земли
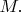
Раньше Вы не учитывали кин. энергию Земли, и это слагаемое терялось. А теперь мы видим, что в законе сохранения энергии есть такое слагаемое, если расчёт делается в системе отсчёта, где начальная скорость Земли

не равна нулю; оно не зависит от

и поэтому не исчезает даже при

А второе слагаемое не зависит от

, но зависит от массы Земли

, причём оно мал
о в меру малости

Поскольку у нас

то теперь мы переходим к приближённому выражению, отбрасывая малое слагаемое, зависящее от массы Земли:

В этом приближении закон сохранения энергии принимает следующий вид:

Для чего он нам нужен? Мы используем его как уравнение для нахождения начальной скорости ракеты

такой, что далеко от Земли (где энергия взаимного притяжения ракеты и Земли в разумном приближении будет пренебрежимо мала) скорость ракеты в данной системе отсчёта будет равна заданной величине

На всякий случай поясню ещё раз, что из этого уравнения мы не "доказываем" никакого утверждения про скорость

Ведь наука не знает: будет человек запускать с Земли ракету или не будет, а если будет, то с какой скоростью он её запустит. Если запустит с очень маленькой скоростью относительно Земли, то ракета лишь чуть-чуть взлетит и шлёпнется обратно на Землю; к этому случаю наше уравнение не имеет отношения, так как в уравнении предполагается, что ракета в конце-концов улетает сколь угодно далеко от Земли. А другой раз человек захочет запустить ракету с такой скоростью

чтобы в дали от Земли (говоря приближённо -"на бесконечности", где притяжение уже не чувствуется) ракета продолжала бы лететь по инерции с заданной скоростью

например, тысяча км/сек относительно системы отсчёта, в которой Земля двигалась в начальный момент, например, со скоростью

сто км/сек.
Должно быть понятно, что существует сколько хочешь таких постановок задач: задается конкретная начальная скорость Земли (и затем она играет роль константы, характеризующей заданную систему отсчёта), и задаётся в этой же системе отсчёта конкретная желаемая скорость полёта ракеты по инерции "на бесконечности", а необходимую для этого начальную скорость ракеты надо вычислить.
Так вот, допустим, как частный случай такой задачи, мы задаём условия: пусть в как-то выбранной системе отсчёта начальная скорость Земли есть заданный вектор

а желаемая скорость ракеты "на бесконечности" в той же системе отсчёта пусть совпадает с этим вектором:

Какую начальную скорость

должна иметь ракета в этом случае? Наше уравнение для этого случая принимает следующий вид:

Чтобы его решить, запишем неизвестный вектор

в виде суммы нового неизвестного вектора

и заданного вектора

то есть:

Физ. смысл нового неизвестного вектора, как видим, простой:

есть скорость ракеты относительно Земли в начальный момент времени. Подставив указанную сумму в уравнение, получаем:

и, после раскрытия скобок:

Найденная отсюда величина

есть 2-я космическая скорость: это найденная в разумном приближении
минимальная скорость ракеты (относительно Земли), которую надо придать ракете вблизи Земли, чтобы ракета смогла, преодолев притяжение, удалиться "на бесконечность". Действительно, из уравнения видно, что если в него подставить меньшую величину скорости, то левая часть уже будет отрицательной, то есть она не сможет быть нулём или равняться какой-нибудь положительной величине

Если же подставить в уравнение большую величину скорости, чем указанная минимальная

, то левая часть будет равна какой-то положительной величине — физически это означает, что ракета в этом случае улетает "на бесконечность" и продолжает там лететь с ненулевой скоростью.
Наконец, замечание о скорости Земли в конечный момент времени в этой задаче. Из закона сохранения импульса мы видим, что разность конечной и начальной скорости Земли

зависит от массы Земли

и является малой в меру малости

Мы решали приближённое уравнение для космической скорости - в нём в разности кин. энергий Земли было отброшено слагаемое, зависящие от массы Земли, как если бы Земля была бесконечно массивной в смысле своих динамических свойств (но в потенциальной энергии гравитационного взаимодействия с ракетой массу Земли, разумеется, нельзя полагать бесконечной). Поэтому приближённое уравнение для космической скорости больше не испортится от того, что мы, перейдя к пределу

будем считать, что приближённо




