Признаю, что в конце предыдущего сообщения я выразился слишком жёстко (сейчас отредактировал). В "подробном" решении, которое я привёл раньше, самом по себе ошибок нет. Но в нём была принята простейшая модель:
Теперь сделаем упрощающее предположение: предположим, что ракета в процессе своего полёта прочь от Земли и Солнца почти не изменяет их внутреннюю энергию, а только немножко изменяет скорость движения их центра масс (и поэтому векторы

и

чуть-чуть различаются). То есть, предполагаю, что приближённо выполняется равенство

Вот тут и "зарыта собака". Если предположить обратное, а именно, что ракета передаёт заметную часть своей энергии во "внутреннюю энергию" Земли с Солнцем, то закон сохранения энергии запишется в виде (вместо



Так как Солнце намного массивнее Земли, то можно предположить, что внутренняя энергия системы "Солнце + Земля" изменяется в основном за счёт изменения кинетической энергии Земли (в системе покоя центра масс "Земля + Солнце", поскольку здесь речь идёт о внутренней энергии; или, что практически то же, в системе покоя Солнца). И происходит это, в основном, пока ракета ещё не слишком удалилась от Земли: пока сила взаимодействия ракеты с Землёй больше, чем с Солнцем, то и передача импульса Земле больше. Если предположить для оценки, что это происходит, когда ракета теряет скорость от начальной

до "солнечной параболической"

где

и считать, что при этом ракета передаёт импульс только Земле, то получим:

Величины скоростей взяты в системе покоя Солнца, так как она с хорошей точностью совпадает с системой центра масс "Солнце + Земля"; предполагается, что векторы скоростей здесь направлены одинаково. В системе покоя Солнца можно считать, что

и тогда
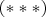
в системе покоя Солнца при

сводится к уравнению:

Это уравнение для 3-й космической скорости

с обозначениями

можно переписать и в такой форме:

Здесь

имеет смысл 3-й космической скорости в системе покоя Земли. С учётом известных значений обитальной скорости Земли

и 2-й космической скорости

отсюда

Так мне видится разгадка ответа "16". Насколько этот вывод близок тому, чему нас учит
Uchitel'_istorii, не берусь судить.